Rotation Invariant Angular Descriptor Via A Bandlimited Gaussian-like Kernel

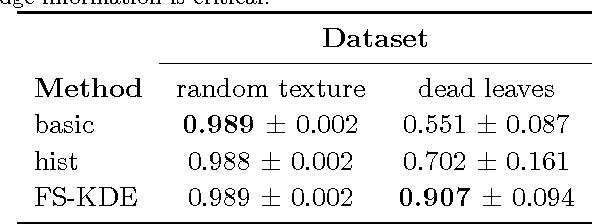
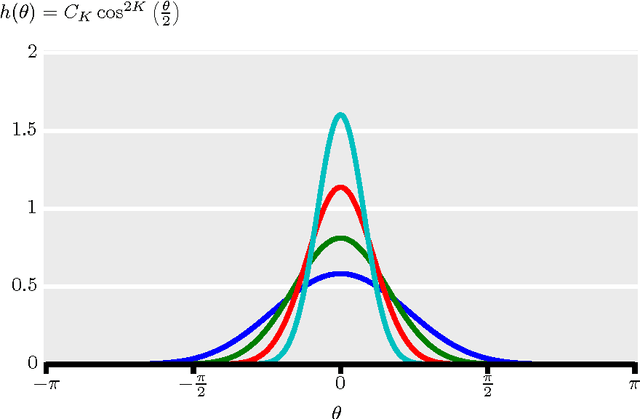
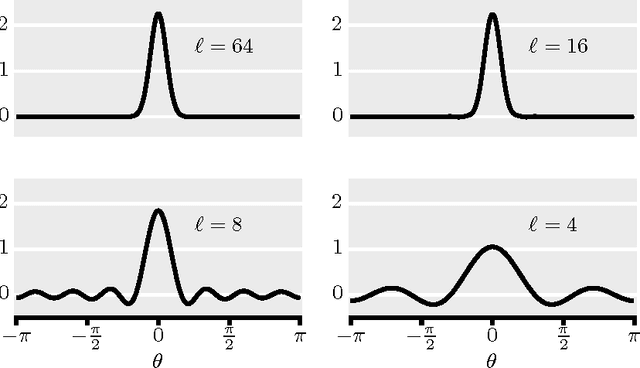
We present a new smooth, Gaussian-like kernel that allows the kernel density estimate for an angular distribution to be exactly represented by a finite number of its Fourier series coefficients. Distributions of angular quantities, such as gradients, are a central part of several state-of-the-art image processing algorithms, but these distributions are usually described via histograms and therefore lack rotation invariance due to binning artifacts. Replacing histograming with kernel density estimation removes these binning artifacts and can provide a finite-dimensional descriptor of the distribution, provided that the kernel is selected to be bandlimited. In this paper, we present a new band-limited kernel that has the added advantage of being Gaussian-like in the angular domain. We then show that it compares favorably to gradient histograms for patch matching, person detection, and texture segmentation.

Guaranteeing Convergence of Iterative Skewed Voting Algorithms for Image Segmentation

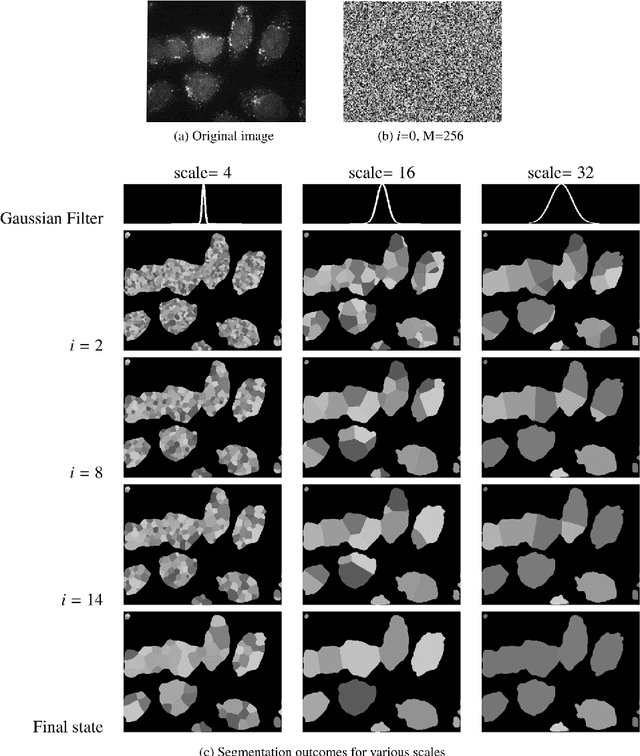
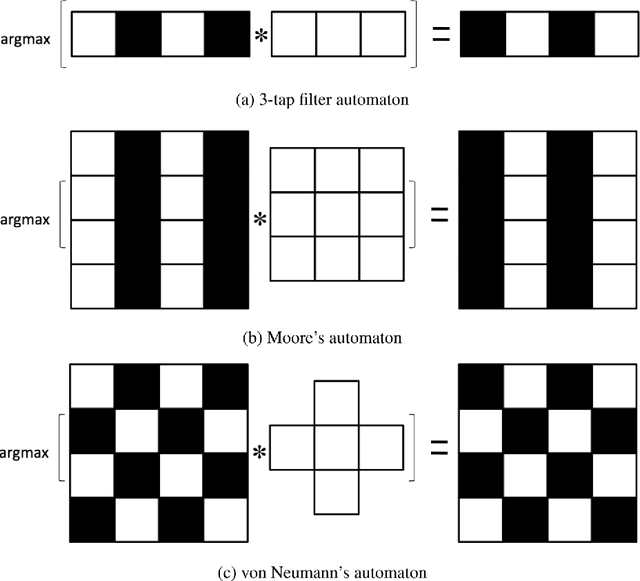
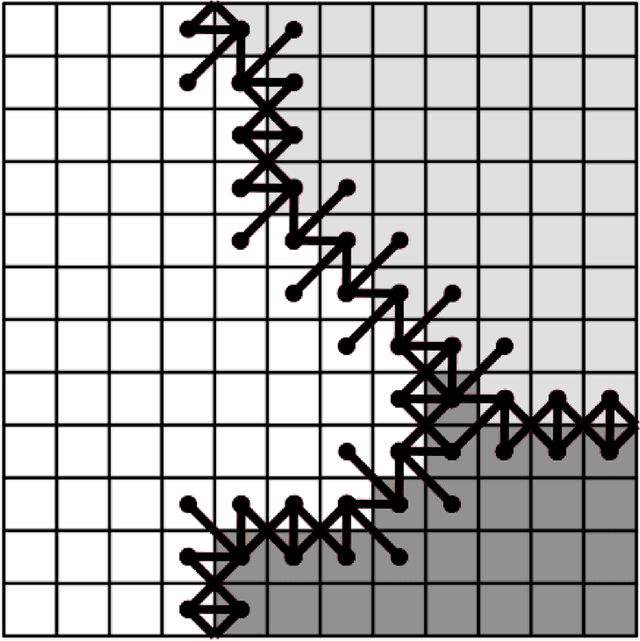
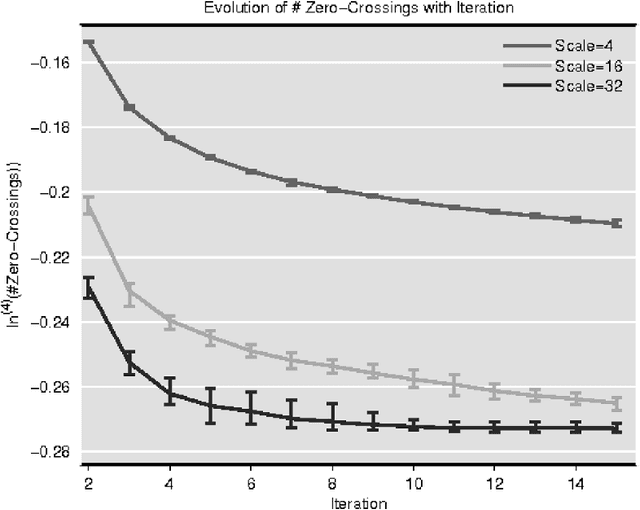
In this paper we provide rigorous proof for the convergence of an iterative voting-based image segmentation algorithm called Active Masks. Active Masks (AM) was proposed to solve the challenging task of delineating punctate patterns of cells from fluorescence microscope images. Each iteration of AM consists of a linear convolution composed with a nonlinear thresholding; what makes this process special in our case is the presence of additive terms whose role is to "skew" the voting when prior information is available. In real-world implementation, the AM algorithm always converges to a fixed point. We study the behavior of AM rigorously and present a proof of this convergence. The key idea is to formulate AM as a generalized (parallel) majority cellular automaton, adapting proof techniques from discrete dynamical systems.