R-FUSE: Robust Fast Fusion of Multi-Band Images Based on Solving a Sylvester Equation

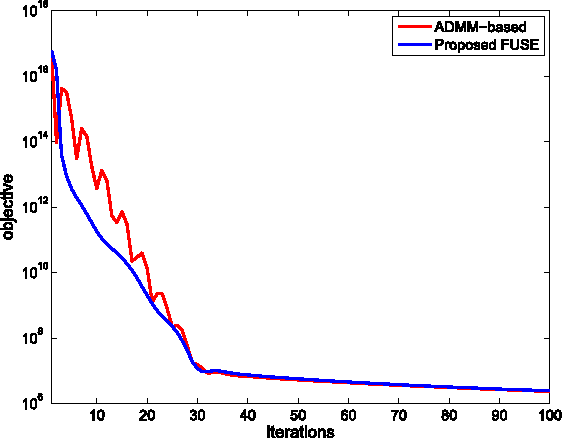
This paper proposes a robust fast multi-band image fusion method to merge a high-spatial low-spectral resolution image and a low-spatial high-spectral resolution image. Following the method recently developed in [1], the generalized Sylvester matrix equation associated with the multi-band image fusion problem is solved in a more robust and efficient way by exploiting the Woodbury formula, avoiding any permutation operation in the frequency domain as well as the blurring kernel invertibility assumption required in [1]. Thanks to this improvement, the proposed algorithm requires fewer computational operations and is also more robust with respect to the blurring kernel compared with the one in [1]. The proposed new algorithm is tested with different priors considered in [1]. Our conclusion is that the proposed fusion algorithm is more robust than the one in [1] with a reduced computational cost.

Multi-Band Image Fusion Based on Spectral Unmixing

This paper presents a multi-band image fusion algorithm based on unsupervised spectral unmixing for combining a high-spatial low-spectral resolution image and a low-spatial high-spectral resolution image. The widely used linear observation model (with additive Gaussian noise) is combined with the linear spectral mixture model to form the likelihoods of the observations. The non-negativity and sum-to-one constraints resulting from the intrinsic physical properties of the abundances are introduced as prior information to regularize this ill-posed problem. The joint fusion and unmixing problem is then formulated as maximizing the joint posterior distribution with respect to the endmember signatures and abundance maps, This optimization problem is attacked with an alternating optimization strategy. The two resulting sub-problems are convex and are solved efficiently using the alternating direction method of multipliers. Experiments are conducted for both synthetic and semi-real data. Simulation results show that the proposed unmixing based fusion scheme improves both the abundance and endmember estimation comparing with the state-of-the-art joint fusion and unmixing algorithms.

Performance measures for classification systems with rejection

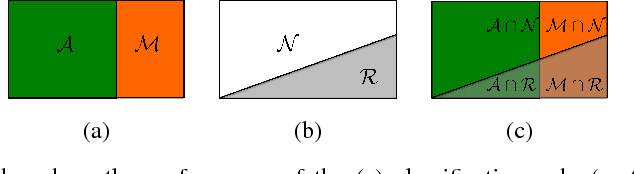
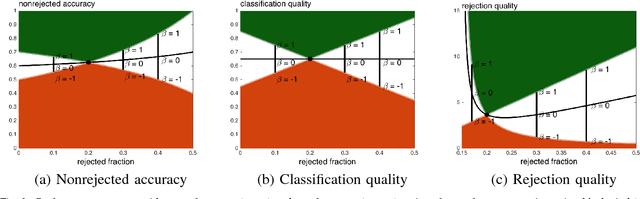
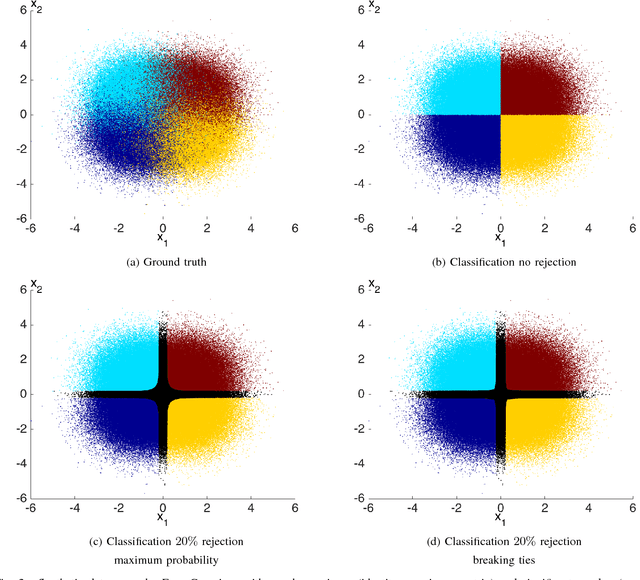
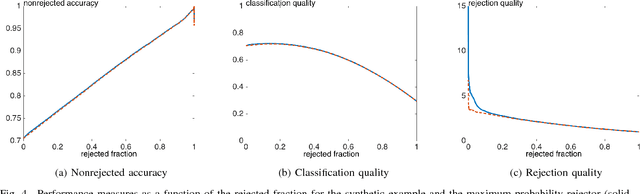
Classifiers with rejection are essential in real-world applications where misclassifications and their effects are critical. However, if no problem specific cost function is defined, there are no established measures to assess the performance of such classifiers. We introduce a set of desired properties for performance measures for classifiers with rejection, based on which we propose a set of three performance measures for the evaluation of the performance of classifiers with rejection that satisfy the desired properties. The nonrejected accuracy measures the ability of the classifier to accurately classify nonrejected samples; the classification quality measures the correct decision making of the classifier with rejector; and the rejection quality measures the ability to concentrate all misclassified samples onto the set of rejected samples. From the measures, we derive the concept of relative optimality that allows us to connect the measures to a family of cost functions that take into account the trade-off between rejection and misclassification. We illustrate the use of the proposed performance measures on classifiers with rejection applied to synthetic and real-world data.

Fast Spectral Unmixing based on Dykstra's Alternating Projection

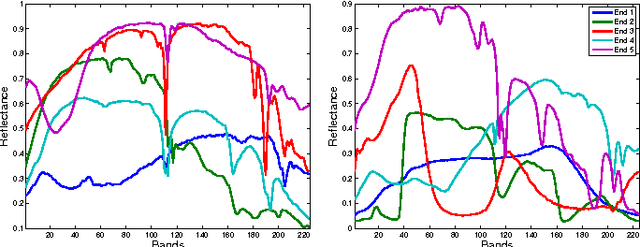
This paper presents a fast spectral unmixing algorithm based on Dykstra's alternating projection. The proposed algorithm formulates the fully constrained least squares optimization problem associated with the spectral unmixing task as an unconstrained regression problem followed by a projection onto the intersection of several closed convex sets. This projection is achieved by iteratively projecting onto each of the convex sets individually, following Dyktra's scheme. The sequence thus obtained is guaranteed to converge to the sought projection. Thanks to the preliminary matrix decomposition and variable substitution, the projection is implemented intrinsically in a subspace, whose dimension is very often much lower than the number of bands. A benefit of this strategy is that the order of the computational complexity for each projection is decreased from quadratic to linear time. Numerical experiments considering diverse spectral unmixing scenarios provide evidence that the proposed algorithm competes with the state-of-the-art, namely when the number of endmembers is relatively small, a circumstance often observed in real hyperspectral applications.

Robust hyperspectral image classification with rejection fields

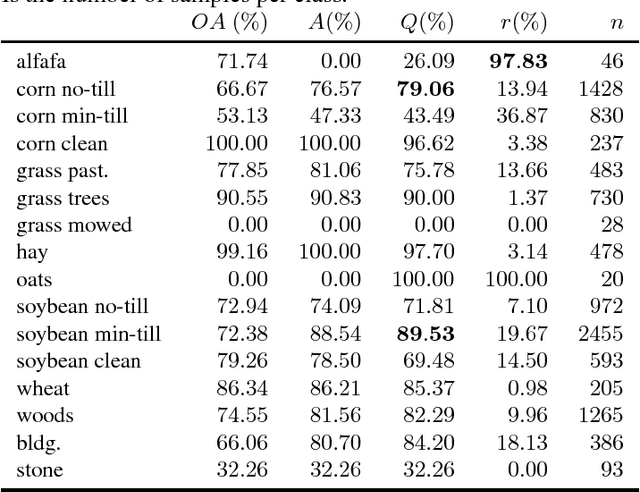
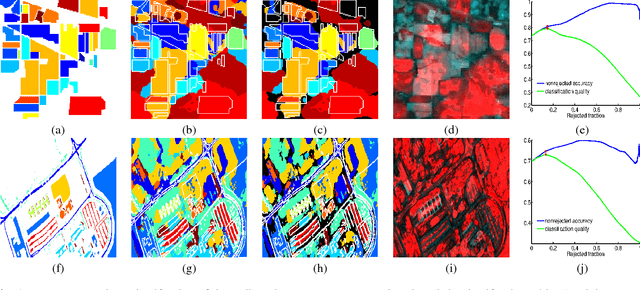
In this paper we present a novel method for robust hyperspectral image classification using context and rejection. Hyperspectral image classification is generally an ill-posed image problem where pixels may belong to unknown classes, and obtaining representative and complete training sets is costly. Furthermore, the need for high classification accuracies is frequently greater than the need to classify the entire image. We approach this problem with a robust classification method that combines classification with context with classification with rejection. A rejection field that will guide the rejection is derived from the classification with contextual information obtained by using the SegSALSA algorithm. We validate our method in real hyperspectral data and show that the performance gains obtained from the rejection fields are equivalent to an increase the dimension of the training sets.

SegSALSA-STR: A convex formulation to supervised hyperspectral image segmentation using hidden fields and structure tensor regularization

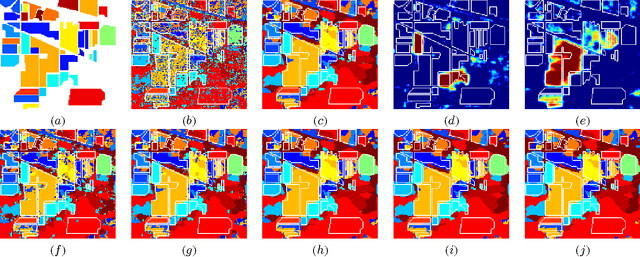
We present a supervised hyperspectral image segmentation algorithm based on a convex formulation of a marginal maximum a posteriori segmentation with hidden fields and structure tensor regularization: Segmentation via the Constraint Split Augmented Lagrangian Shrinkage by Structure Tensor Regularization (SegSALSA-STR). This formulation avoids the generally discrete nature of segmentation problems and the inherent NP-hardness of the integer optimization associated. We extend the Segmentation via the Constraint Split Augmented Lagrangian Shrinkage (SegSALSA) algorithm by generalizing the vectorial total variation prior using a structure tensor prior constructed from a patch-based Jacobian. The resulting algorithm is convex, time-efficient and highly parallelizable. This shows the potential of combining hidden fields with convex optimization through the inclusion of different regularizers. The SegSALSA-STR algorithm is validated in the segmentation of real hyperspectral images.