Deep Learning reconstruction with uncertainty estimation for $γ$ photon interaction in fast scintillator detectors

This article presents a physics-informed deep learning method for the quantitative estimation of the spatial coordinates of gamma interactions within a monolithic scintillator, with a focus on Positron Emission Tomography (PET) imaging. A Density Neural Network approach is designed to estimate the 2-dimensional gamma photon interaction coordinates in a fast lead tungstate (PbWO4) monolithic scintillator detector. We introduce a custom loss function to estimate the inherent uncertainties associated with the reconstruction process and to incorporate the physical constraints of the detector. This unique combination allows for more robust and reliable position estimations and the obtained results demonstrate the effectiveness of the proposed approach and highlights the significant benefits of the uncertainties estimation. We discuss its potential impact on improving PET imaging quality and show how the results can be used to improve the exploitation of the model, to bring benefits to the application and how to evaluate the validity of the given prediction and the associated uncertainties. Importantly, our proposed methodology extends beyond this specific use case, as it can be generalized to other applications beyond PET imaging.

Packed-Ensembles for Efficient Uncertainty Estimation

Deep Ensembles (DE) are a prominent approach achieving excellent performance on key metrics such as accuracy, calibration, uncertainty estimation, and out-of-distribution detection. However, hardware limitations of real-world systems constrain to smaller ensembles and lower capacity networks, significantly deteriorating their performance and properties. We introduce Packed-Ensembles (PE), a strategy to design and train lightweight structured ensembles by carefully modulating the dimension of their encoding space. We leverage grouped convolutions to parallelize the ensemble into a single common backbone and forward pass to improve training and inference speeds. PE is designed to work under the memory budget of a single standard neural network. Through extensive studies we show that PE faithfully preserve the properties of DE, e.g., diversity, and match their performance in terms of accuracy, calibration, out-of-distribution detection and robustness to distribution shift.

Efficient Seismic fragility curve estimation by Active Learning on Support Vector Machines

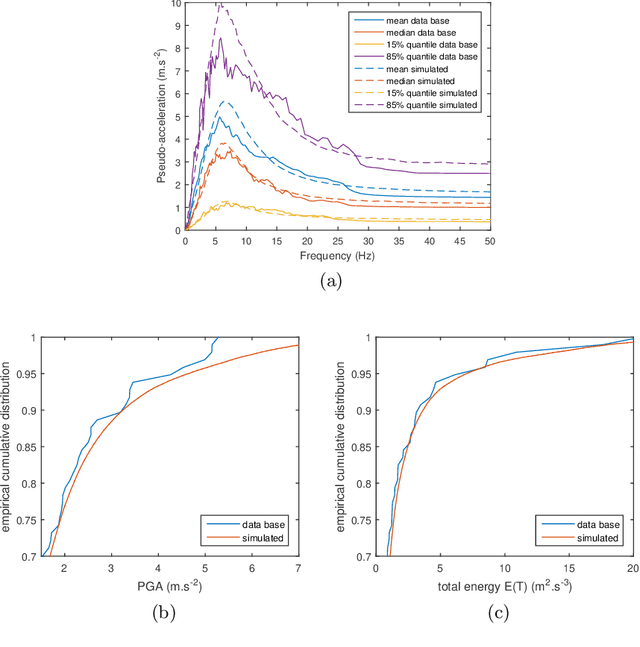
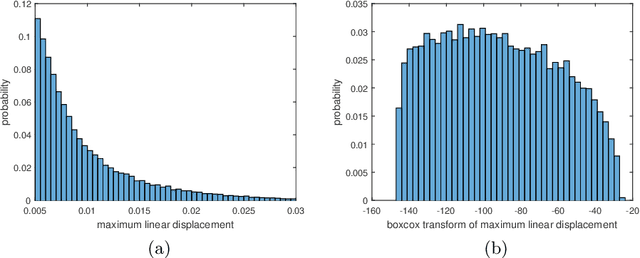
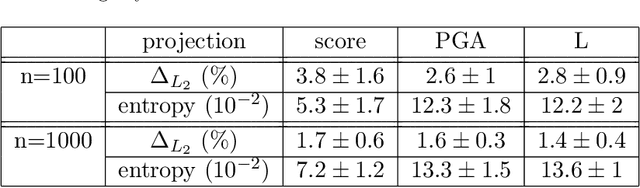
Fragility curves which express the failure probability of a structure, or critical components, as function of a loading intensity measure are nowadays widely used (i) in Seismic Probabilistic Risk Assessment studies, (ii) to evaluate impact of construction details on the structural performance of installations under seismic excitations or under other loading sources such as wind. To avoid the use of parametric models such as lognormal model to estimate fragility curves from a reduced number of numerical calculations, a methodology based on Support Vector Machines coupled with an active learning algorithm is proposed in this paper. In practice, input excitation is reduced to some relevant parameters and, given these parameters, SVMs are used for a binary classification of the structural responses relative to a limit threshold of exceedance. Since the output is not only binary, this is a score, a probabilistic interpretation of the output is exploited to estimate very efficiently fragility curves as score functions or as functions of classical seismic intensity measures.