Speeding Up Image Classifiers with Little Companions

Scaling up neural networks has been a key recipe to the success of large language and vision models. However, in practice, up-scaled models can be disproportionately costly in terms of computations, providing only marginal improvements in performance; for example, EfficientViT-L3-384 achieves <2% improvement on ImageNet-1K accuracy over the base L1-224 model, while requiring $14\times$ more multiply-accumulate operations (MACs). In this paper, we investigate scaling properties of popular families of neural networks for image classification, and find that scaled-up models mostly help with "difficult" samples. Decomposing the samples by difficulty, we develop a simple model-agnostic two-pass Little-Big algorithm that first uses a light-weight "little" model to make predictions of all samples, and only passes the difficult ones for the "big" model to solve. Good little companion achieve drastic MACs reduction for a wide variety of model families and scales. Without loss of accuracy or modification of existing models, our Little-Big models achieve MACs reductions of 76% for EfficientViT-L3-384, 81% for EfficientNet-B7-600, 71% for DeiT3-L-384 on ImageNet-1K. Little-Big also speeds up the InternImage-G-512 model by 62% while achieving 90% ImageNet-1K top-1 accuracy, serving both as a strong baseline and as a simple practical method for large model compression.

Merlin: Enabling Machine Learning-Ready HPC Ensembles

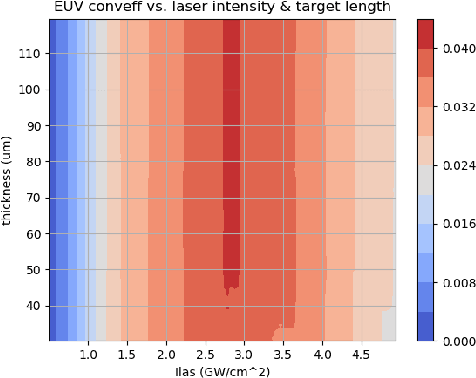
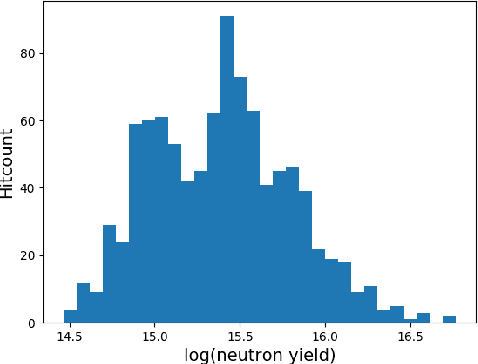
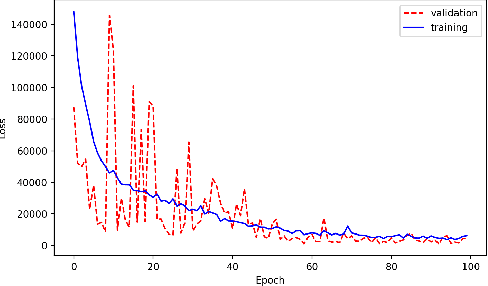
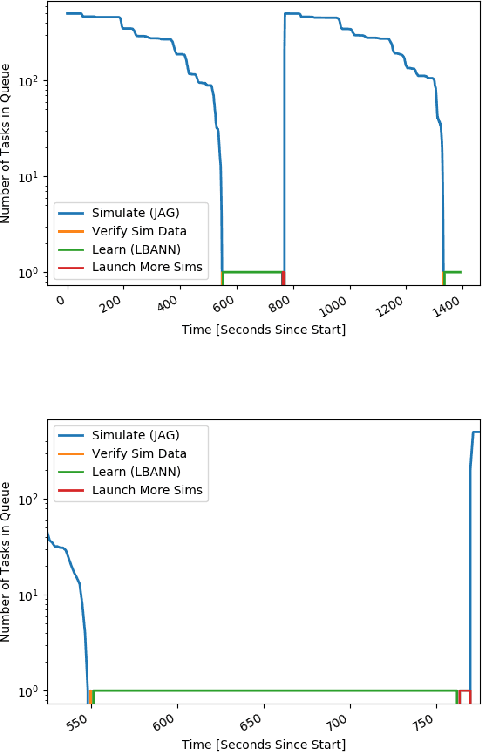
With the growing complexity of computational and experimental facilities, many scientific researchers are turning to machine learning (ML) techniques to analyze large scale ensemble data. With complexities such as multi-component workflows, heterogeneous machine architectures, parallel file systems, and batch scheduling, care must be taken to facilitate this analysis in a high performance computing (HPC) environment. In this paper, we present Merlin, a workflow framework to enable large ML-friendly ensembles of scientific HPC simulations. By augmenting traditional HPC with distributed compute technologies, Merlin aims to lower the barrier for scientific subject matter experts to incorporate ML into their analysis. In addition to its design and some examples, we describe how Merlin was deployed on the Sierra Supercomputer at Lawrence Livermore National Laboratory to create an unprecedented benchmark inertial confinement fusion dataset of approximately 100 million individual simulations and over 24 terabytes of multi-modal physics-based scalar, vector and hyperspectral image data.

Efficient Data-Driven Geologic Feature Detection from Pre-stack Seismic Measurements using Randomized Machine-Learning Algorithm

Conventional seismic techniques for detecting the subsurface geologic features are challenged by limited data coverage, computational inefficiency, and subjective human factors. We developed a novel data-driven geological feature detection approach based on pre-stack seismic measurements. Our detection method employs an efficient and accurate machine-learning detection approach to extract useful subsurface geologic features automatically. Specifically, our method is based on kernel ridge regression model. The conventional kernel ridge regression can be computationally prohibited because of the large volume of seismic measurements. We employ a data reduction technique in combination with the conventional kernel ridge regression method to improve the computational efficiency and reduce memory usage. In particular, we utilize a randomized numerical linear algebra technique, named Nystr\"om method, to effectively reduce the dimensionality of the feature space without compromising the information content required for accurate detection. We provide thorough computational cost analysis to show efficiency of our new geological feature detection methods. We further validate the performance of our new subsurface geologic feature detection method using synthetic surface seismic data for 2D acoustic and elastic velocity models. Our numerical examples demonstrate that our new detection method significantly improves the computational efficiency while maintaining comparable accuracy. Interestingly, we show that our method yields a speed-up ratio on the order of $\sim10^2$ to $\sim 10^3$ in a multi-core computational environment.