Javier Borquez
DualGuard MPPI: Safe and Performant Optimal Control by Combining Sampling-Based MPC and Hamilton-Jacobi Reachability
Feb 04, 2025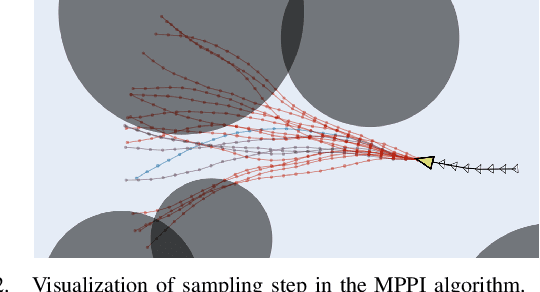
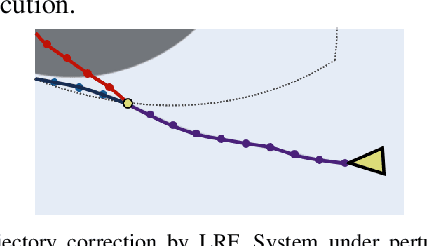
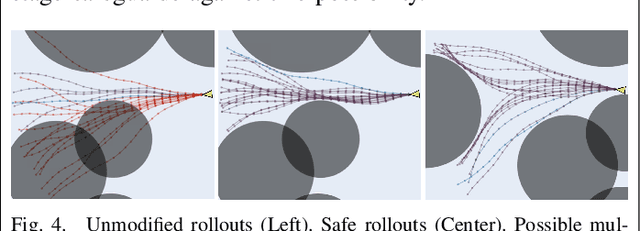
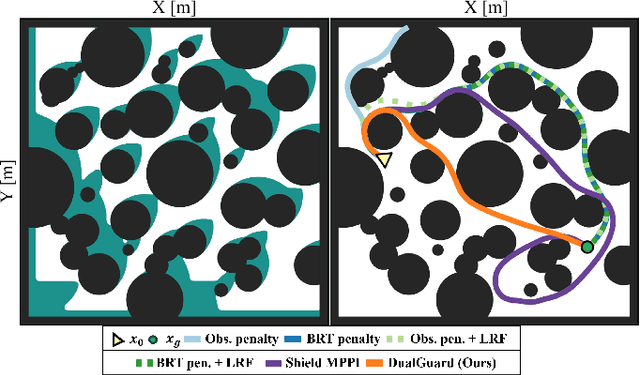
Abstract:Designing controllers that are both safe and performant is inherently challenging. This co-optimization can be formulated as a constrained optimal control problem, where the cost function represents the performance criterion and safety is specified as a constraint. While sampling-based methods, such as Model Predictive Path Integral (MPPI) control, have shown great promise in tackling complex optimal control problems, they often struggle to enforce safety constraints. To address this limitation, we propose DualGuard-MPPI, a novel framework for solving safety-constrained optimal control problems. Our approach integrates Hamilton-Jacobi reachability analysis within the MPPI sampling process to ensure that all generated samples are provably safe for the system. On the one hand, this integration allows DualGuard-MPPI to enforce strict safety constraints; at the same time, it facilitates a more effective exploration of the environment with the same number of samples, reducing the effective sampling variance and leading to better performance optimization. Through several simulations and hardware experiments, we demonstrate that the proposed approach achieves much higher performance compared to existing MPPI methods, without compromising safety.
Providing Safety Assurances for Systems with Unknown Dynamics
Mar 09, 2024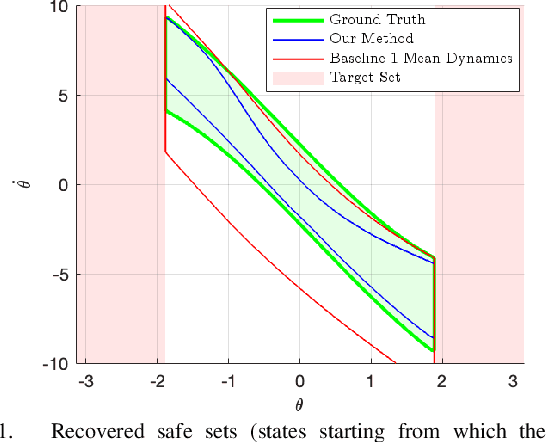
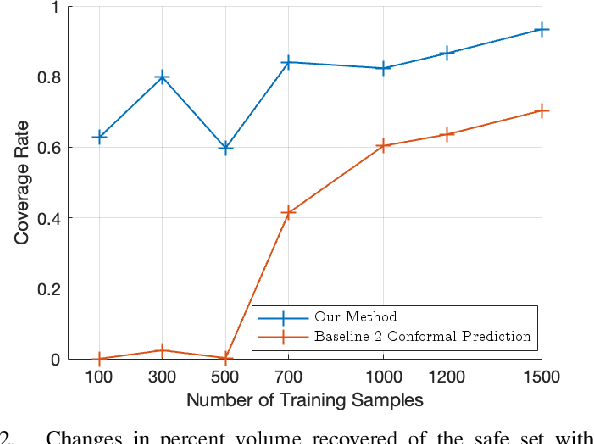
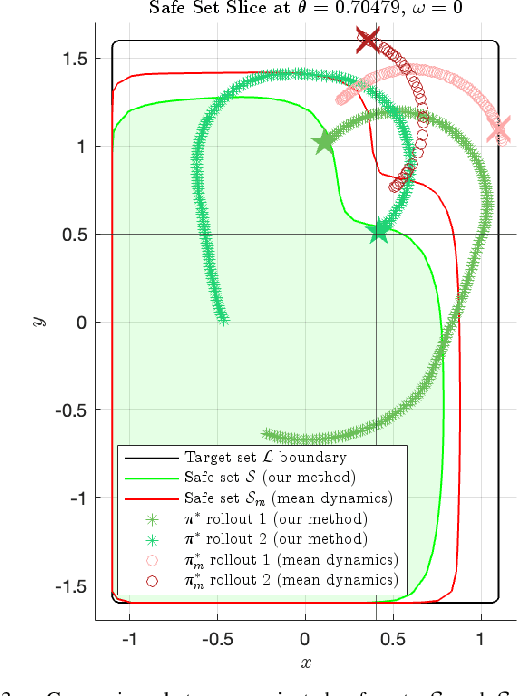
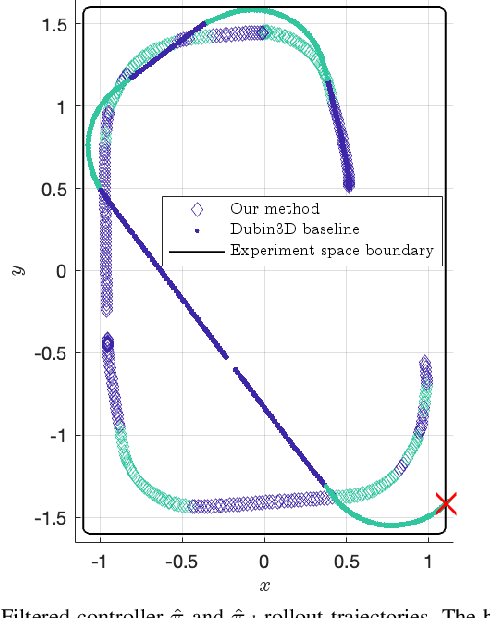
Abstract:As autonomous systems become more complex and integral in our society, the need to accurately model and safely control these systems has increased significantly. In the past decade, there has been tremendous success in using deep learning techniques to model and control systems that are difficult to model using first principles. However, providing safety assurances for such systems remains difficult, partially due to the uncertainty in the learned model. In this work, we aim to provide safety assurances for systems whose dynamics are not readily derived from first principles and, hence, are more advantageous to be learned using deep learning techniques. Given the system of interest and safety constraints, we learn an ensemble model of the system dynamics from data. Leveraging ensemble uncertainty as a measure of uncertainty in the learned dynamics model, we compute a maximal robust control invariant set, starting from which the system is guaranteed to satisfy the safety constraints under the condition that realized model uncertainties are contained in the predefined set of admissible model uncertainty. We demonstrate the effectiveness of our method using a simulated case study with an inverted pendulum and a hardware experiment with a TurtleBot. The experiments show that our method robustifies the control actions of the system against model uncertainty and generates safe behaviors without being overly restrictive. The codes and accompanying videos can be found on the project website.
On Safety and Liveness Filtering Using Hamilton-Jacobi Reachability Analysis
Dec 23, 2023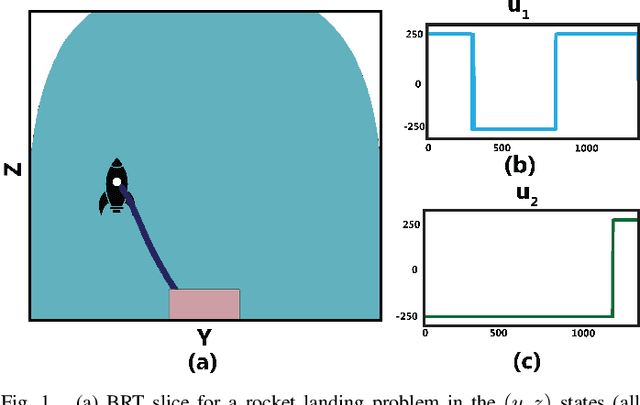
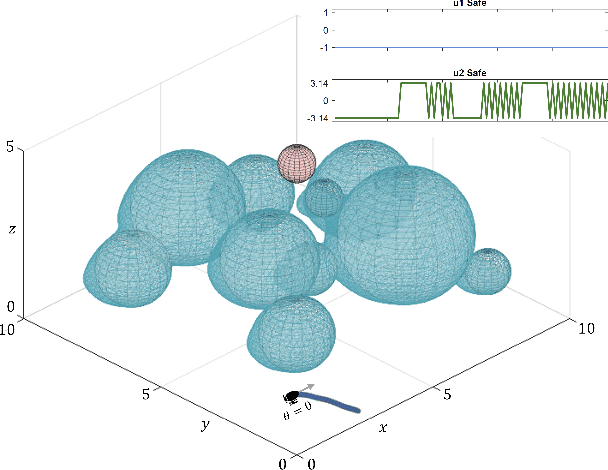
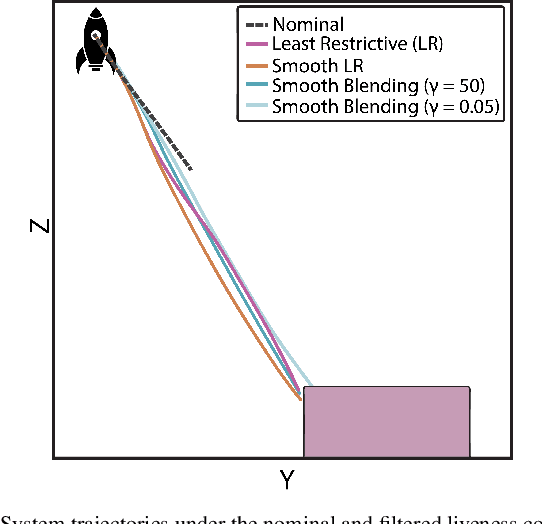
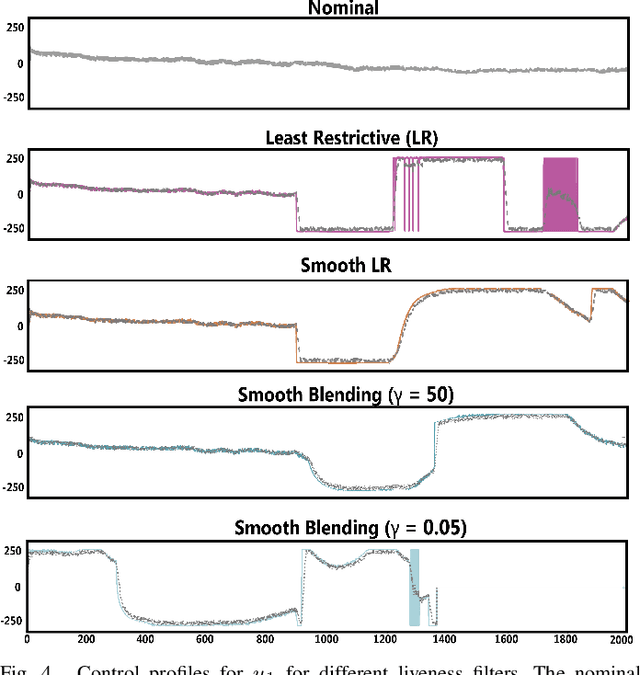
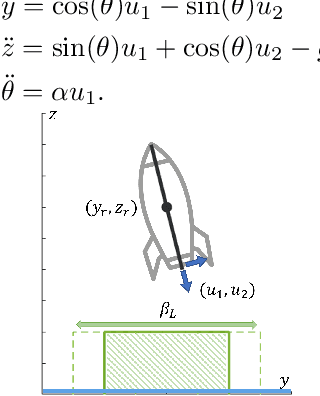
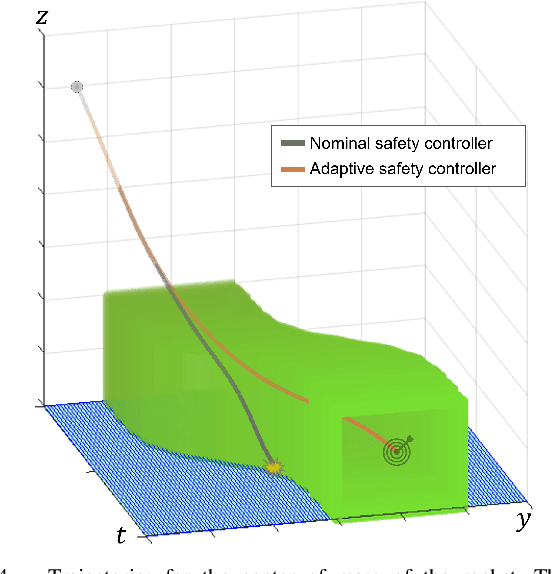
Abstract:Hamilton-Jacobi (HJ) reachability-based filtering provides a powerful framework to co-optimize performance and safety (or liveness) for autonomous systems. Under this filtering scheme, a nominal controller is minimally modified to ensure system safety or liveness. However, the resulting controllers can exhibit abrupt switching and bang-bang behavior, which is not suitable for applications of autonomous systems in the real world. This work presents a novel, unifying framework to design safety and liveness filters through reachability analysis. We explicitly characterize the maximal set of control inputs that ensures safety (or liveness) at a given state. Different safety filters can then be constructed using different subsets of this maximal set along with a projection operator to modify the nominal controller. We use the proposed framework to design three safety filters, each balancing performance, computation time, and smoothness differently. The proposed filters can easily handle dynamics uncertainties, disturbances, and bounded control inputs. We highlight their relative strengths and limitations by applying these filters to autonomous navigation and rocket landing scenarios and on a physical robot testbed. We also discuss practical aspects associated with implementing these filters on real-world autonomous systems. Our research advances the understanding and potential application of reachability-based controllers on real-world autonomous systems.
Hamilton-Jacobi Reachability Analysis for Hybrid Systems with Controlled and Forced Transitions
Sep 19, 2023Abstract:Hybrid dynamical systems with non-linear dynamics are one of the most general modeling tools for representing robotic systems, especially contact-rich systems. However, providing guarantees regarding the safety or performance of such hybrid systems can still prove to be a challenging problem because it requires simultaneous reasoning about continuous state evolution and discrete mode switching. In this work, we address this problem by extending classical Hamilton-Jacobi (HJ) reachability analysis, a formal verification method for continuous non-linear dynamics in the presence of bounded inputs and disturbances, to hybrid dynamical systems. Our framework can compute reachable sets for hybrid systems consisting of multiple discrete modes, each with its own set of non-linear continuous dynamics, discrete transitions that can be directly commanded or forced by a discrete control input, while still accounting for control bounds and adversarial disturbances in the state evolution. Along with the reachable set, the proposed framework also provides an optimal continuous and discrete controller to ensure system safety. We demonstrate our framework in simulation on an aircraft collision avoidance problem, as well as on a real-world testbed to solve the optimal mode planning problem for a quadruped with multiple gaits.
Parameter-Conditioned Reachable Sets for Updating Safety Assurances Online
Sep 29, 2022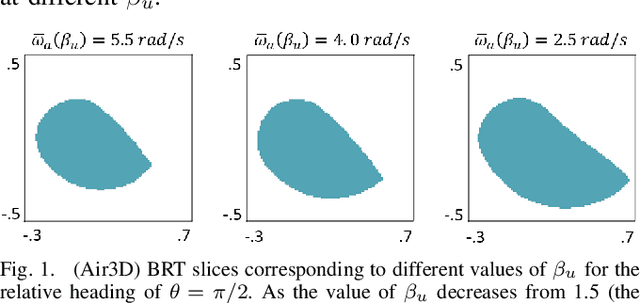
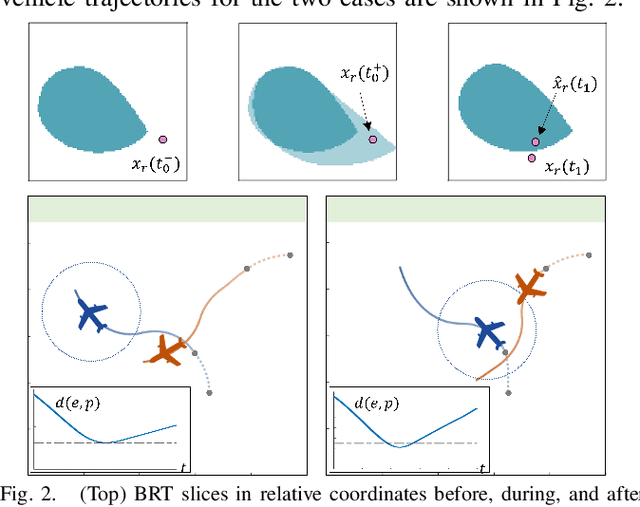
Abstract:Hamilton-Jacobi (HJ) reachability analysis is a powerful tool for analyzing the safety of autonomous systems. However, the provided safety assurances are often predicated on the assumption that once deployed, the system or its environment does not evolve. Online, however, an autonomous system might experience changes in system dynamics, control authority, external disturbances, and/or the surrounding environment, requiring updated safety assurances. Rather than restarting the safety analysis from scratch, which can be time-consuming and often intractable to perform online, we propose to compute \textit{parameter-conditioned} reachable sets. Assuming expected system and environment changes can be parameterized, we treat these parameters as virtual states in the system and leverage recent advances in high-dimensional reachability analysis to solve the corresponding reachability problem offline. This results in a family of reachable sets that is parameterized by the environment and system factors. Online, as these factors change, the system can simply query the corresponding safety function from this family to ensure system safety, enabling a real-time update of the safety assurances. Through various simulation studies, we demonstrate the capability of our approach in maintaining system safety despite the system and environment evolution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge