Jaroslaw Rzepecki
Fast Neural Network based Solving of Partial Differential Equations
May 27, 2022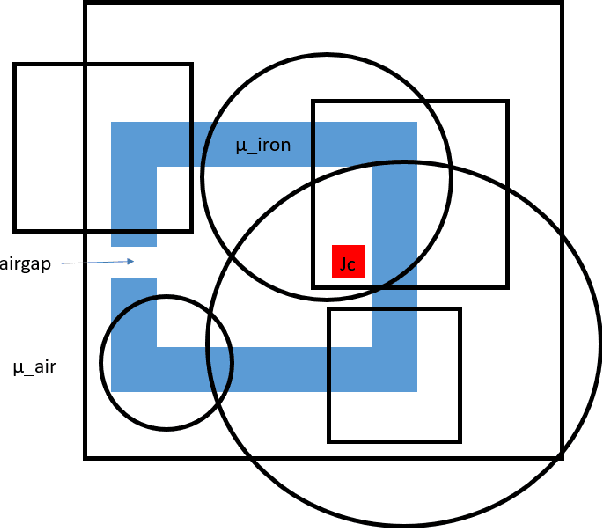

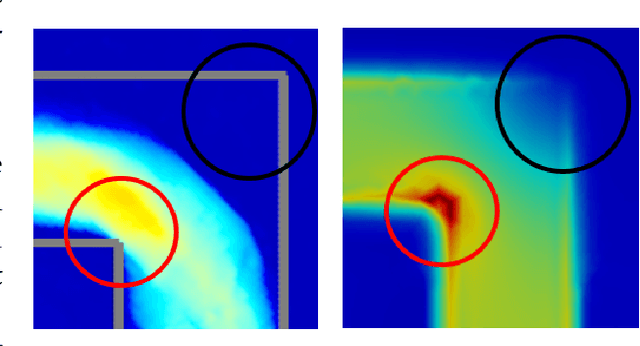
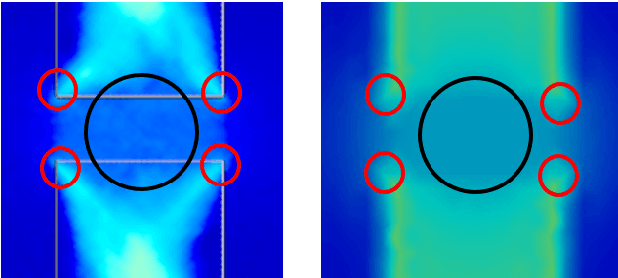
Abstract:We present a novel method for using Neural Networks (NNs) for finding solutions to a class of Partial Differential Equations (PDEs). Our method builds on recent advances in Neural Radiance Field research (NeRFs) and allows for a NN to converge to a PDE solution much faster than classic Physically Informed Neural Network (PINNs) approaches.
Navigation Turing Test (NTT): Learning to Evaluate Human-Like Navigation
May 20, 2021



Abstract:A key challenge on the path to developing agents that learn complex human-like behavior is the need to quickly and accurately quantify human-likeness. While human assessments of such behavior can be highly accurate, speed and scalability are limited. We address these limitations through a novel automated Navigation Turing Test (ANTT) that learns to predict human judgments of human-likeness. We demonstrate the effectiveness of our automated NTT on a navigation task in a complex 3D environment. We investigate six classification models to shed light on the types of architectures best suited to this task, and validate them against data collected through a human NTT. Our best models achieve high accuracy when distinguishing true human and agent behavior. At the same time, we show that predicting finer-grained human assessment of agents' progress towards human-like behavior remains unsolved. Our work takes an important step towards agents that more effectively learn complex human-like behavior.
Near-Optimal Online Egalitarian learning in General Sum Repeated Matrix Games
Jun 04, 2019
Abstract:We study two-player general sum repeated finite games where the rewards of each player are generated from an unknown distribution. Our aim is to find the egalitarian bargaining solution (EBS) for the repeated game, which can lead to much higher rewards than the maximin value of both players. Our most important contribution is the derivation of an algorithm that achieves simultaneously, for both players, a high-probability regret bound of order $\mathcal{O}(\sqrt[3]{\ln T}\cdot T^{2/3})$ after any $T$ rounds of play. We demonstrate that our upper bound is nearly optimal by proving a lower bound of $\Omega(T^{2/3})$ for any algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge