Fast Neural Network based Solving of Partial Differential Equations

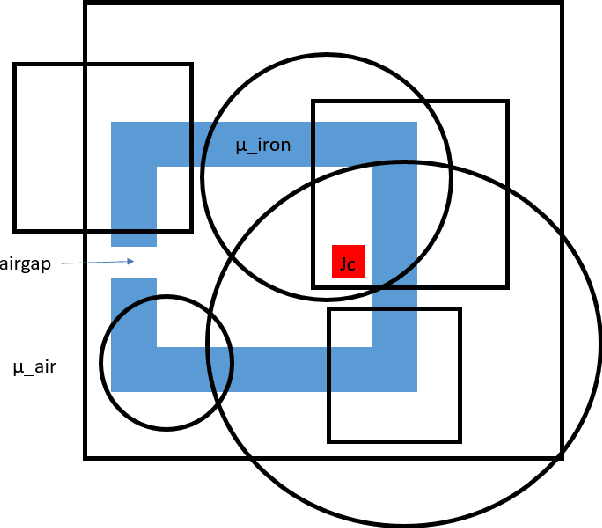
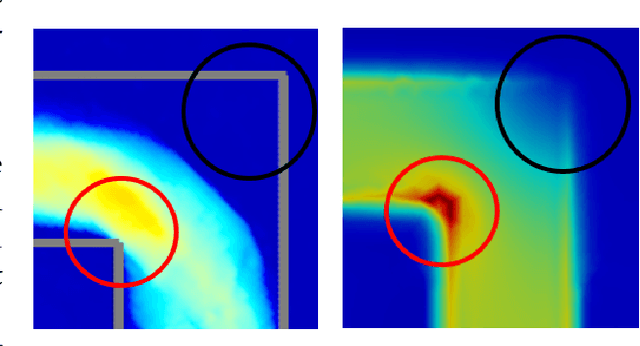
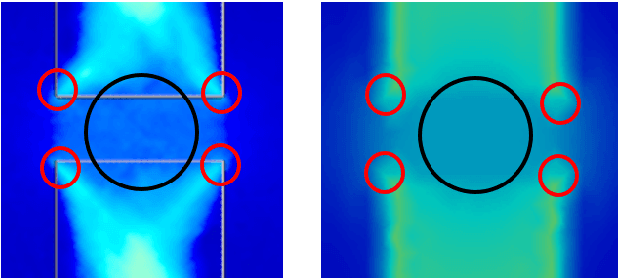
We present a novel method for using Neural Networks (NNs) for finding solutions to a class of Partial Differential Equations (PDEs). Our method builds on recent advances in Neural Radiance Field research (NeRFs) and allows for a NN to converge to a PDE solution much faster than classic Physically Informed Neural Network (PINNs) approaches.

Dynamical Pose Estimation

We study the problem of aligning two sets of 3D geometric primitives given known correspondences. Our first contribution is to show that this primitive alignment framework unifies five perception problems including point cloud registration, primitive (mesh) registration, category-level 3D registration, absolution pose estimation (APE), and category-level APE. Our second contribution is to propose DynAMical Pose estimation (DAMP), the first general and practical algorithm to solve primitive alignment problem by simulating rigid body dynamics arising from virtual springs and damping, where the springs span the shortest distances between corresponding primitives. Our third contribution is to apply DAMP to the five perception problems in simulated and real datasets and demonstrate (i) DAMP always converges to the globally optimal solution in the first three problems with 3D-3D correspondences; (ii) although DAMP sometimes converges to suboptimal solutions in the last two problems with 2D-3D correspondences, with a simple scheme for escaping local minima, DAMP almost always succeeds. Our last contribution is to demystify the surprising empirical performance of DAMP and formally prove a global convergence result in the case of point cloud registration by charactering local stability of the equilibrium points of the underlying dynamical system.