Two-phase Optimization of Binary Sequences with Low Peak Sidelobe Level Value

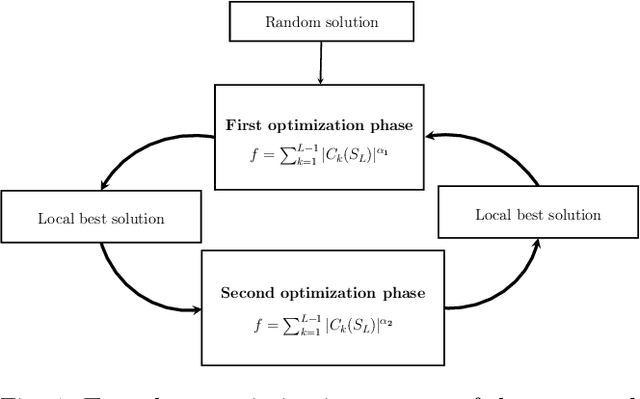
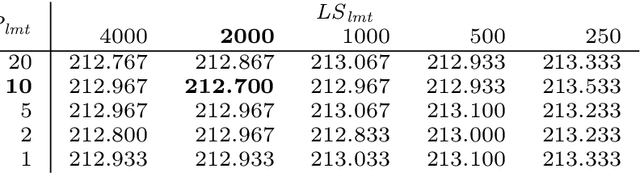
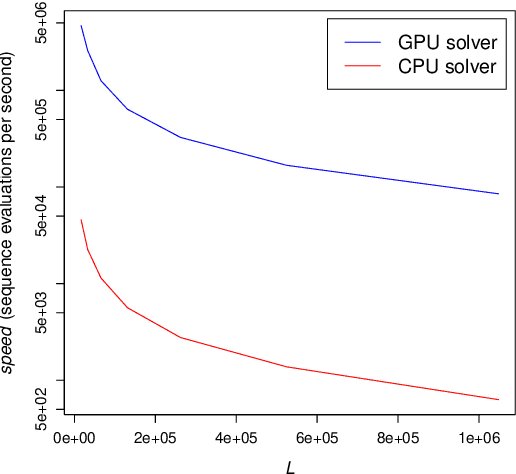
The search for binary sequences with low peak sidelobe level value represents a formidable computational problem. To locate better sequences for this problem, we designed a stochastic algorithm that uses two fitness functions. In these fitness functions, the value of the autocorrelation function has a different impact on the final fitness value. It is defined with the value of the exponent over the autocorrelation function values. Each function is used in the corresponding optimization phase, and the optimization process switches between these two phases until the stopping condition is satisfied. The proposed algorithm was implemented using the compute unified device architecture and therefore allowed us to exploit the computational power of graphics processing units. This algorithm was tested on sequences with lengths $L = 2^m - 1$, for $14 \le m \le 20$. From the obtained results it is evident that the usage of two fitness functions improved the efficiency of the algorithm significantly, new-best known solutions were achieved, and the achieved PSL values were significantly less than $\sqrt{L}$.

Two-level protein folding optimization on a three-dimensional AB off-lattice model

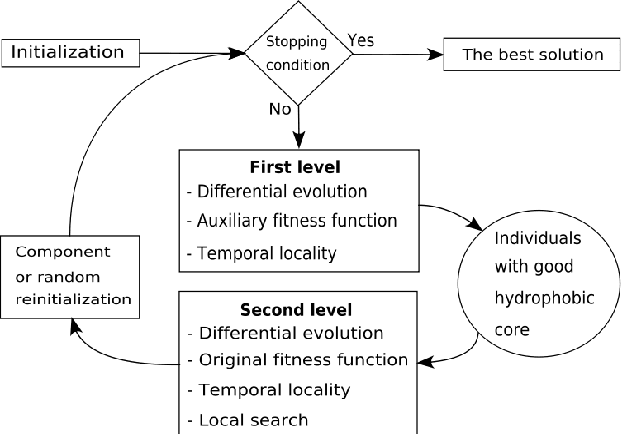
This paper presents a two-level protein folding optimization on a three-dimensional AB off-lattice model. The first level is responsible for forming conformations with a good hydrophobic core or a set of compact hydrophobic amino acid positions. These conformations are forwarded to the second level, where an accurate search is performed with the aim of locating conformations with the best energy value. The optimization process switches between these two levels until the stopping condition is satisfied. An auxiliary fitness function was designed for the first level, while the original fitness function is used in the second level. The auxiliary fitness function includes expression about the quality of the hydrophobic core. This expression is crucial for leading the search process to the promising solutions that have a good hydrophobic core and, consequently, improves the efficiency of the whole optimization process. Our differential evolution algorithm was used for demonstrating the efficiency of the two-level optimization. It was analyzed on well-known amino acid sequences that are used frequently in the literature. The obtained experimental results show that the employed two-level optimization improves the efficiency of our algorithm significantly, and that the proposed algorithm is superior to other state-of-the-art algorithms.

Protein Folding Optimization using Differential Evolution Extended with Local Search and Component Reinitialization

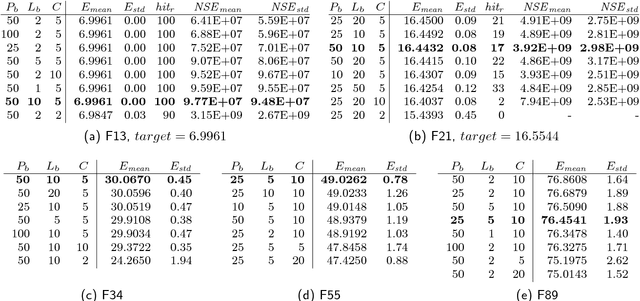
This paper presents a novel Differential Evolution algorithm for protein folding optimization that is applied to a three-dimensional AB off-lattice model. The proposed algorithm includes two new mechanisms. A local search is used to improve convergence speed and to reduce the runtime complexity of the energy calculation. For this purpose, a local movement is introduced within the local search. The designed evolutionary algorithm has fast convergence speed and, therefore, when it is trapped into the local optimum or a relatively good solution is located, it is hard to locate a better similar solution. The similar solution is different from the good solution in only a few components. A component reinitialization method is designed to mitigate this problem. Both the new mechanisms and the proposed algorithm were analyzed on well-known amino acid sequences that are used frequently in the literature. Experimental results show that the employed new mechanisms improve the efficiency of our algorithm and that the proposed algorithm is superior to other state-of-the-art algorithms. It obtained a hit ratio of 100% for sequences up to 18 monomers, within a budget of $10^{11}$ solution evaluations. New best-known solutions were obtained for most of the sequences. The existence of the symmetric best-known solutions is also demonstrated in the paper.

Making up for the deficit in a marathon run

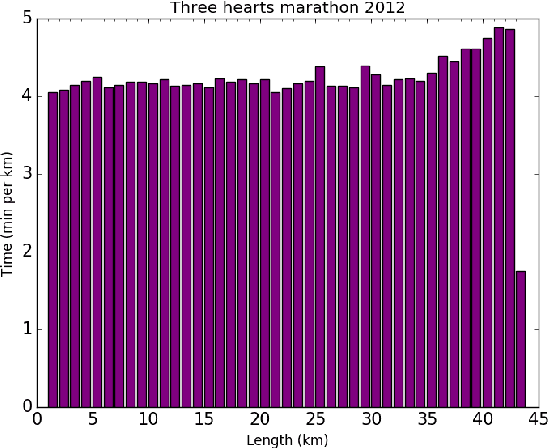
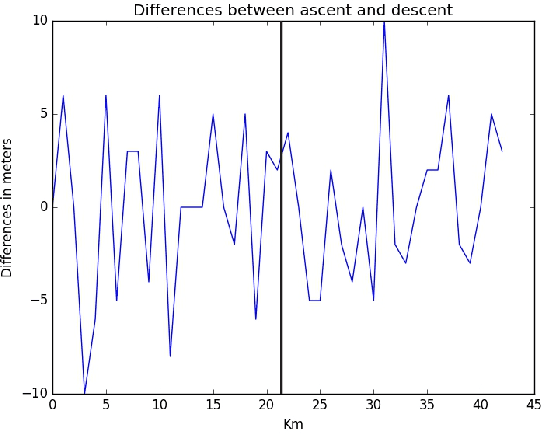
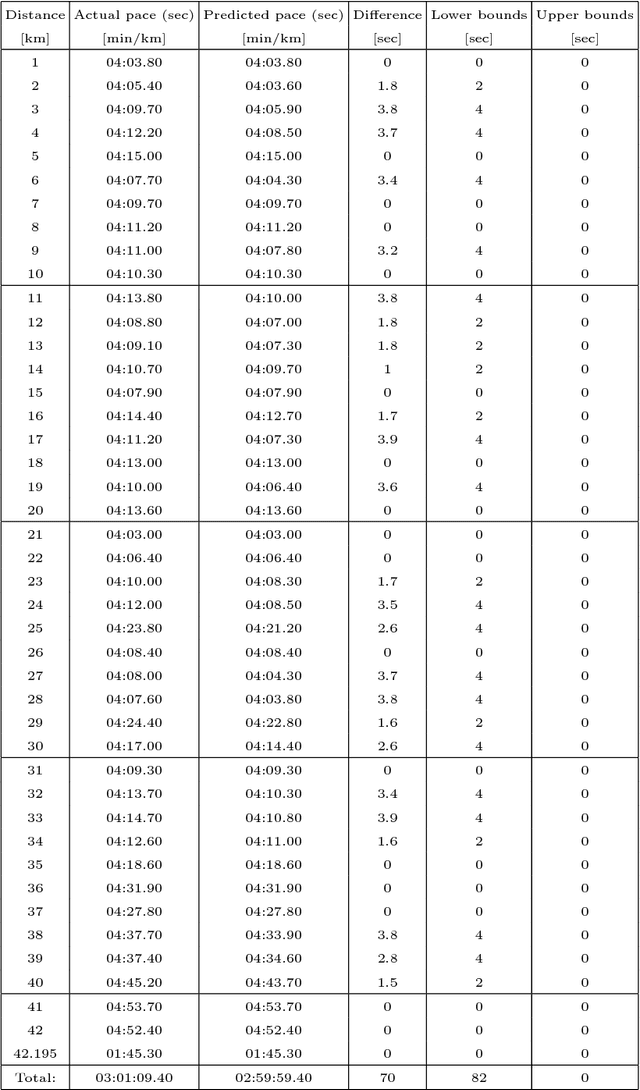
To predict the final result of an athlete in a marathon run thoroughly is the eternal desire of each trainer. Usually, the achieved result is weaker than the predicted one due to the objective (e.g., environmental conditions) as well as subjective factors (e.g., athlete's malaise). Therefore, making up for the deficit between predicted and achieved results is the main ingredient of the analysis performed by trainers after the competition. In the analysis, they search for parts of a marathon course where the athlete lost time. This paper proposes an automatic making up for the deficit by using a Differential Evolution algorithm. In this case study, the results that were obtained by a wearable sports-watch by an athlete in a real marathon are analyzed. The first experiments with Differential Evolution show the possibility of using this method in the future.

Low-Autocorrelation Binary Sequences: On Improved Merit Factors and Runtime Predictions to Achieve Them

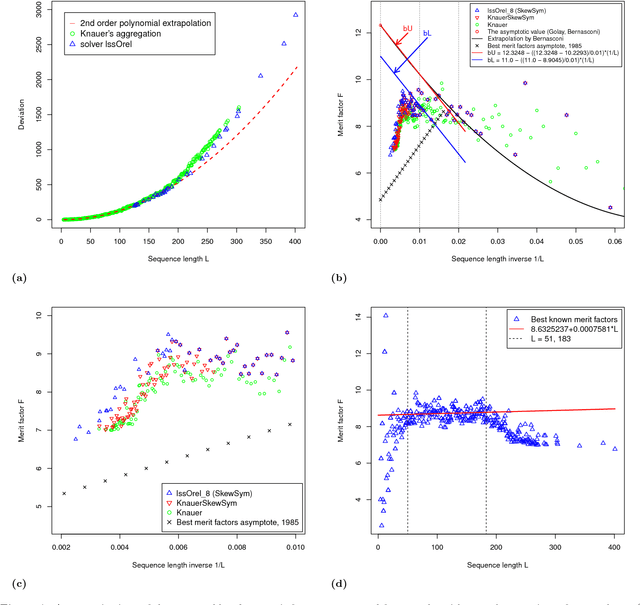
The search for binary sequences with a high figure of merit, known as the low autocorrelation binary sequence ($labs$}) problem, represents a formidable computational challenge. To mitigate the computational constraints of the problem, we consider solvers that accept odd values of sequence length $L$ and return solutions for skew-symmetric binary sequences only -- with the consequence that not all best solutions under this constraint will be optimal for each $L$. In order to improve both, the search for best merit factor $and$ the asymptotic runtime performance, we instrumented three stochastic solvers, the first two are state-of-the-art solvers that rely on variants of memetic and tabu search ($lssMAts$ and $lssRRts$), the third solver ($lssOrel$) organizes the search as a sequence of independent contiguous self-avoiding walk segments. By adapting a rigorous statistical methodology to performance testing of all three combinatorial solvers, experiments show that the solver with the best asymptotic average-case performance, $lssOrel\_8 = 0.000032*1.1504^L$, has the best chance of finding solutions that improve, as $L$ increases, figures of merit reported to date. The same methodology can be applied to engineering new $labs$ solvers that may return merit factors even closer to the conjectured asymptotic value of 12.3248.

A comprehensive review of firefly algorithms

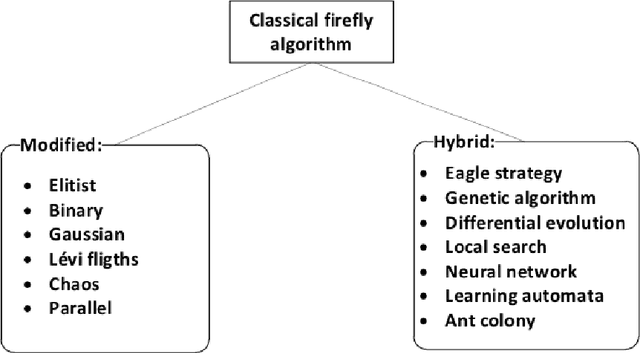
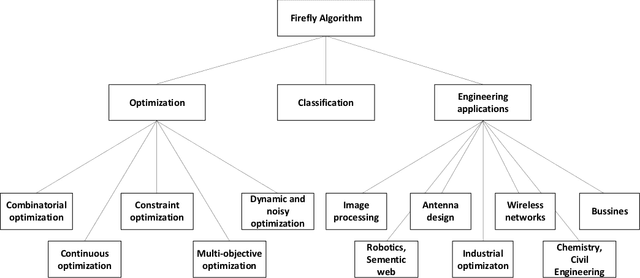
The firefly algorithm has become an increasingly important tool of Swarm Intelligence that has been applied in almost all areas of optimization, as well as engineering practice. Many problems from various areas have been successfully solved using the firefly algorithm and its variants. In order to use the algorithm to solve diverse problems, the original firefly algorithm needs to be modified or hybridized. This paper carries out a comprehensive review of this living and evolving discipline of Swarm Intelligence, in order to show that the firefly algorithm could be applied to every problem arising in practice. On the other hand, it encourages new researchers and algorithm developers to use this simple and yet very efficient algorithm for problem solving. It often guarantees that the obtained results will meet the expectations.

A Brief Review of Nature-Inspired Algorithms for Optimization

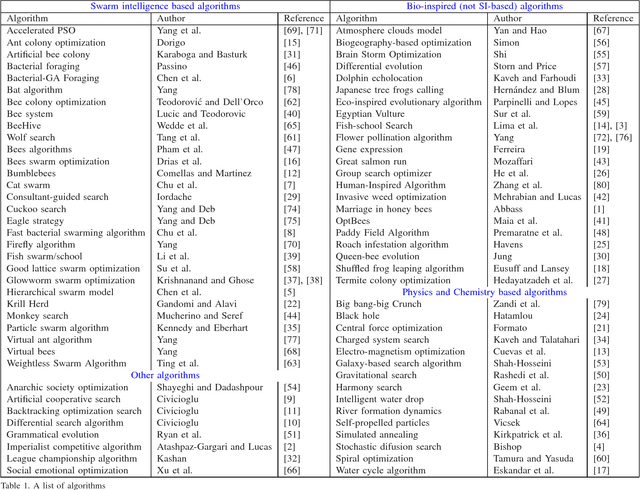
Swarm intelligence and bio-inspired algorithms form a hot topic in the developments of new algorithms inspired by nature. These nature-inspired metaheuristic algorithms can be based on swarm intelligence, biological systems, physical and chemical systems. Therefore, these algorithms can be called swarm-intelligence-based, bio-inspired, physics-based and chemistry-based, depending on the sources of inspiration. Though not all of them are efficient, a few algorithms have proved to be very efficient and thus have become popular tools for solving real-world problems. Some algorithms are insufficiently studied. The purpose of this review is to present a relatively comprehensive list of all the algorithms in the literature, so as to inspire further research.

Comparing various regression methods on ensemble strategies in differential evolution

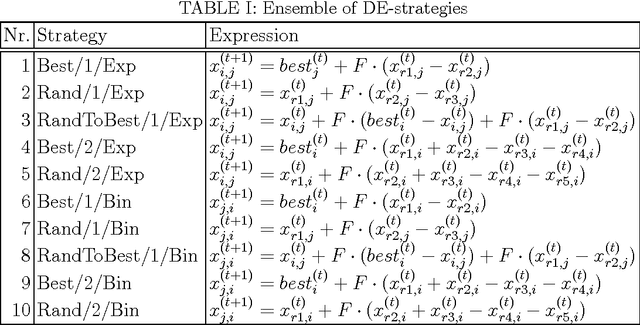
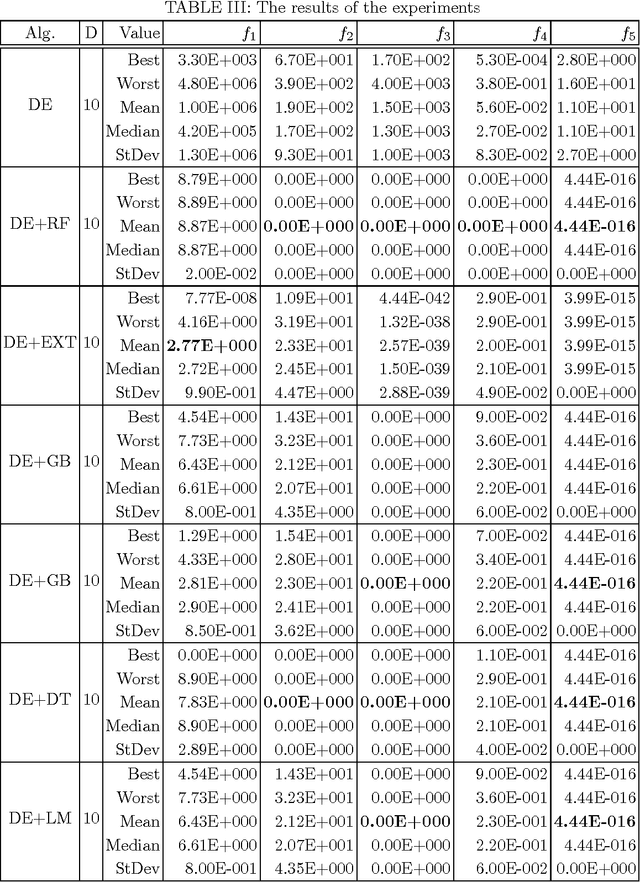
Differential evolution possesses a multitude of various strategies for generating new trial solutions. Unfortunately, the best strategy is not known in advance. Moreover, this strategy usually depends on the problem to be solved. This paper suggests using various regression methods (like random forest, extremely randomized trees, gradient boosting, decision trees, and a generalized linear model) on ensemble strategies in differential evolution algorithm by predicting the best differential evolution strategy during the run. Comparing the preliminary results of this algorithm by optimizing a suite of five well-known functions from literature, it was shown that using the random forest regression method substantially outperformed the results of the other regression methods.

Hybridization of Evolutionary Algorithms

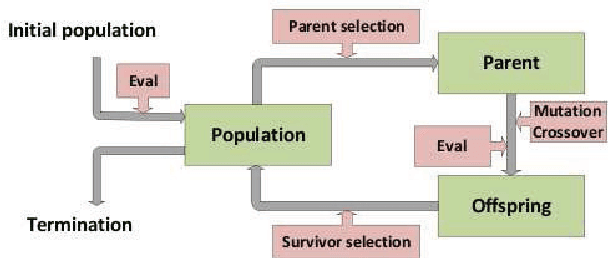
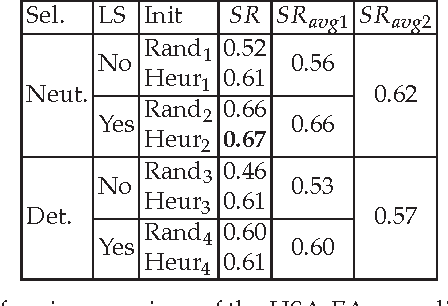
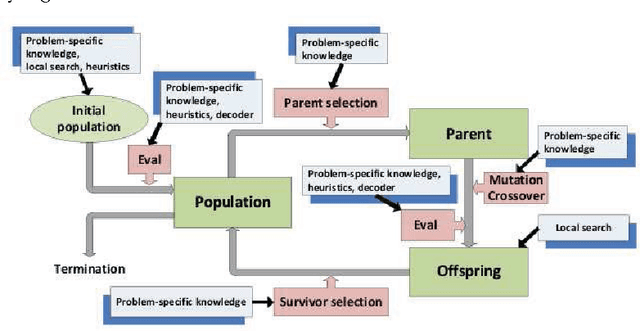
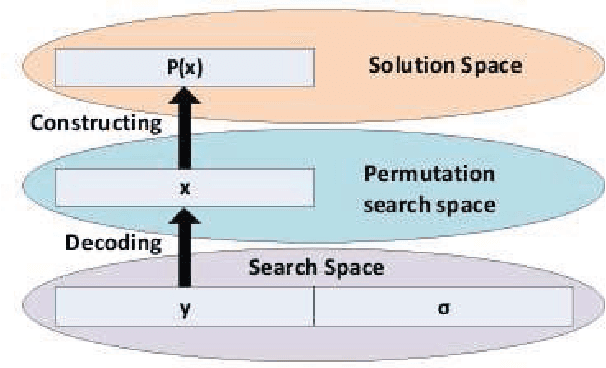
Evolutionary algorithms are good general problem solver but suffer from a lack of domain specific knowledge. However, the problem specific knowledge can be added to evolutionary algorithms by hybridizing. Interestingly, all the elements of the evolutionary algorithms can be hybridized. In this chapter, the hybridization of the three elements of the evolutionary algorithms is discussed: the objective function, the survivor selection operator and the parameter settings. As an objective function, the existing heuristic function that construct the solution of the problem in traditional way is used. However, this function is embedded into the evolutionary algorithm that serves as a generator of new solutions. In addition, the objective function is improved by local search heuristics. The new neutral selection operator has been developed that is capable to deal with neutral solutions, i.e. solutions that have the different representation but expose the equal values of objective function. The aim of this operator is to directs the evolutionary search into a new undiscovered regions of the search space. To avoid of wrong setting of parameters that control the behavior of the evolutionary algorithm, the self-adaptation is used. Finally, such hybrid self-adaptive evolutionary algorithm is applied to the two real-world NP-hard problems: the graph 3-coloring and the optimization of markers in the clothing industry. Extensive experiments shown that these hybridization improves the results of the evolutionary algorithms a lot. Furthermore, the impact of the particular hybridizations is analyzed in details as well.

Using Differential Evolution for the Graph Coloring

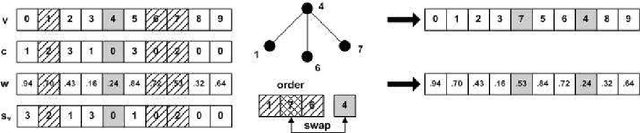
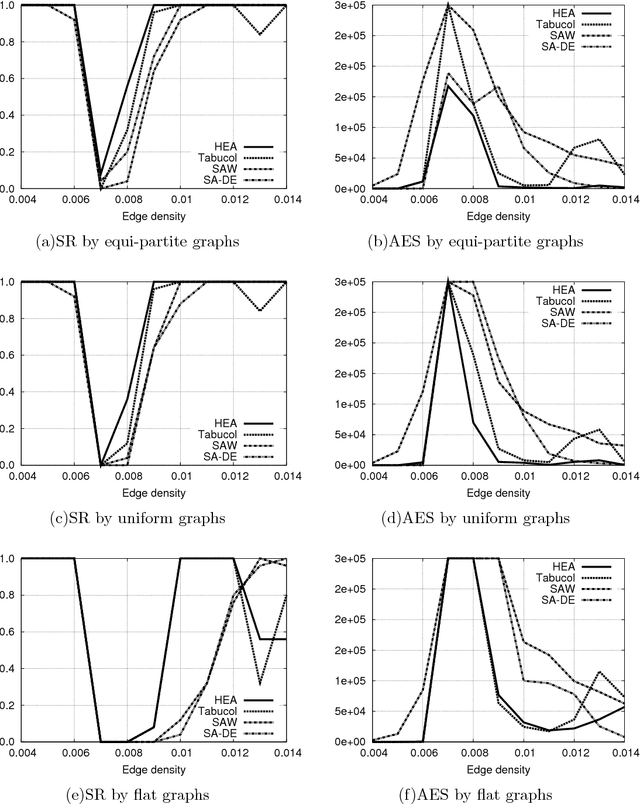
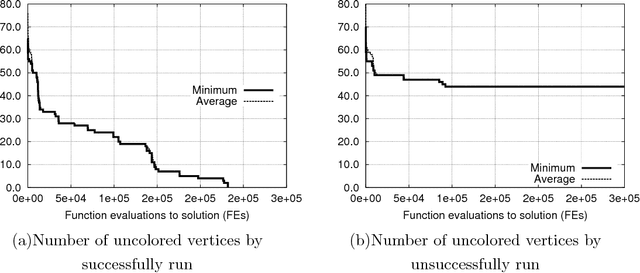
Differential evolution was developed for reliable and versatile function optimization. It has also become interesting for other domains because of its ease to use. In this paper, we posed the question of whether differential evolution can also be used by solving of the combinatorial optimization problems, and in particular, for the graph coloring problem. Therefore, a hybrid self-adaptive differential evolution algorithm for graph coloring was proposed that is comparable with the best heuristics for graph coloring today, i.e. Tabucol of Hertz and de Werra and the hybrid evolutionary algorithm of Galinier and Hao. We have focused on the graph 3-coloring. Therefore, the evolutionary algorithm with method SAW of Eiben et al., which achieved excellent results for this kind of graphs, was also incorporated into this study. The extensive experiments show that the differential evolution could become a competitive tool for the solving of graph coloring problem in the future.