On Uncensored Mean First-Passage-Time Performance Experiments with Multiwalk in $\mathbb{R}^p$: a New Stochastic Optimization Algorithm

A rigorous empirical comparison of two stochastic solvers is important when one of the solvers is a prototype of a new algorithm such as multiwalk (MWA). When searching for global minima in $\mathbb{R}^p$, the key data structures of MWA include: $p$ rulers with each ruler assigned $m$ marks and a set of $p$ neighborhood matrices of size up to $m(m-2)$, where each entry represents absolute values of pairwise differences between $m$ marks. Before taking the next step, a controller links the tableau of neighborhood matrices and computes new and improved positions for each of the $m$ marks. The number of columns in each neighborhood matrix is denoted as the neighborhood radius $r_n \le m-2$. Any variant of the DEA (differential evolution algorithm) has an effective population neighborhood of radius not larger than 1. Uncensored first-passage-time performance experiments that vary the neighborhood radius of a MW-solver can thus be readily compared to existing variants of DE-solvers. The paper considers seven test cases of increasing complexity and demonstrates, under uncensored first-passage-time performance experiments: (1) significant variability in convergence rate for seven DE-based solver configurations, and (2) consistent, monotonic, and significantly faster rate of convergence for the MW-solver prototype as we increase the neighborhood radius from 4 to its maximum value.

Low-Autocorrelation Binary Sequences: On Improved Merit Factors and Runtime Predictions to Achieve Them

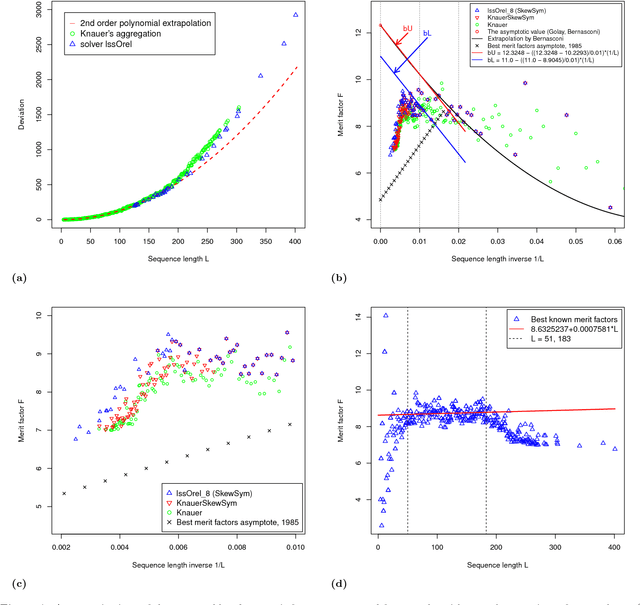
The search for binary sequences with a high figure of merit, known as the low autocorrelation binary sequence ($labs$}) problem, represents a formidable computational challenge. To mitigate the computational constraints of the problem, we consider solvers that accept odd values of sequence length $L$ and return solutions for skew-symmetric binary sequences only -- with the consequence that not all best solutions under this constraint will be optimal for each $L$. In order to improve both, the search for best merit factor $and$ the asymptotic runtime performance, we instrumented three stochastic solvers, the first two are state-of-the-art solvers that rely on variants of memetic and tabu search ($lssMAts$ and $lssRRts$), the third solver ($lssOrel$) organizes the search as a sequence of independent contiguous self-avoiding walk segments. By adapting a rigorous statistical methodology to performance testing of all three combinatorial solvers, experiments show that the solver with the best asymptotic average-case performance, $lssOrel\_8 = 0.000032*1.1504^L$, has the best chance of finding solutions that improve, as $L$ increases, figures of merit reported to date. The same methodology can be applied to engineering new $labs$ solvers that may return merit factors even closer to the conjectured asymptotic value of 12.3248.