Two-phase Optimization of Binary Sequences with Low Peak Sidelobe Level Value

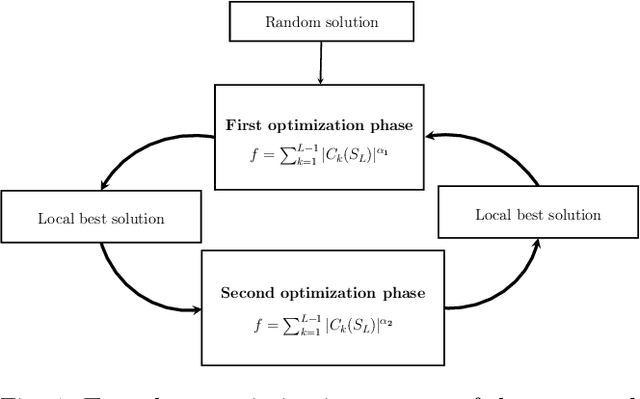
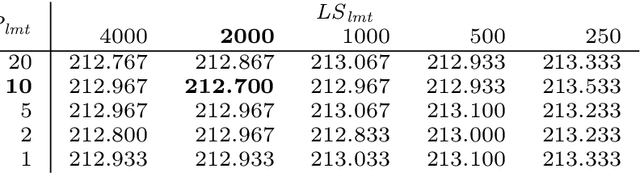
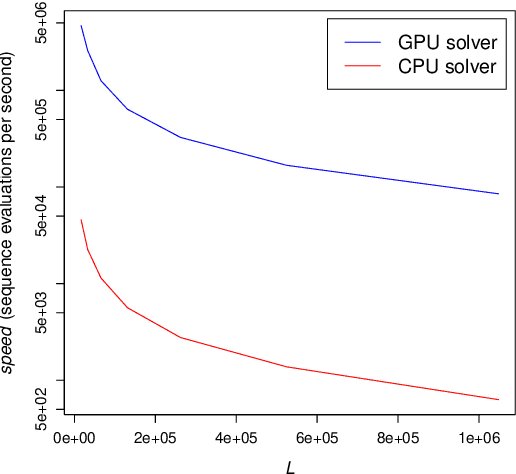
The search for binary sequences with low peak sidelobe level value represents a formidable computational problem. To locate better sequences for this problem, we designed a stochastic algorithm that uses two fitness functions. In these fitness functions, the value of the autocorrelation function has a different impact on the final fitness value. It is defined with the value of the exponent over the autocorrelation function values. Each function is used in the corresponding optimization phase, and the optimization process switches between these two phases until the stopping condition is satisfied. The proposed algorithm was implemented using the compute unified device architecture and therefore allowed us to exploit the computational power of graphics processing units. This algorithm was tested on sequences with lengths $L = 2^m - 1$, for $14 \le m \le 20$. From the obtained results it is evident that the usage of two fitness functions improved the efficiency of the algorithm significantly, new-best known solutions were achieved, and the achieved PSL values were significantly less than $\sqrt{L}$.

Two-level protein folding optimization on a three-dimensional AB off-lattice model

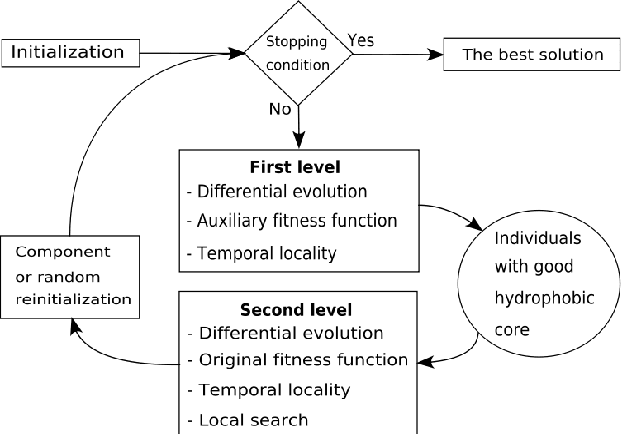
This paper presents a two-level protein folding optimization on a three-dimensional AB off-lattice model. The first level is responsible for forming conformations with a good hydrophobic core or a set of compact hydrophobic amino acid positions. These conformations are forwarded to the second level, where an accurate search is performed with the aim of locating conformations with the best energy value. The optimization process switches between these two levels until the stopping condition is satisfied. An auxiliary fitness function was designed for the first level, while the original fitness function is used in the second level. The auxiliary fitness function includes expression about the quality of the hydrophobic core. This expression is crucial for leading the search process to the promising solutions that have a good hydrophobic core and, consequently, improves the efficiency of the whole optimization process. Our differential evolution algorithm was used for demonstrating the efficiency of the two-level optimization. It was analyzed on well-known amino acid sequences that are used frequently in the literature. The obtained experimental results show that the employed two-level optimization improves the efficiency of our algorithm significantly, and that the proposed algorithm is superior to other state-of-the-art algorithms.

Protein Folding Optimization using Differential Evolution Extended with Local Search and Component Reinitialization

This paper presents a novel Differential Evolution algorithm for protein folding optimization that is applied to a three-dimensional AB off-lattice model. The proposed algorithm includes two new mechanisms. A local search is used to improve convergence speed and to reduce the runtime complexity of the energy calculation. For this purpose, a local movement is introduced within the local search. The designed evolutionary algorithm has fast convergence speed and, therefore, when it is trapped into the local optimum or a relatively good solution is located, it is hard to locate a better similar solution. The similar solution is different from the good solution in only a few components. A component reinitialization method is designed to mitigate this problem. Both the new mechanisms and the proposed algorithm were analyzed on well-known amino acid sequences that are used frequently in the literature. Experimental results show that the employed new mechanisms improve the efficiency of our algorithm and that the proposed algorithm is superior to other state-of-the-art algorithms. It obtained a hit ratio of 100% for sequences up to 18 monomers, within a budget of $10^{11}$ solution evaluations. New best-known solutions were obtained for most of the sequences. The existence of the symmetric best-known solutions is also demonstrated in the paper.

Low-Autocorrelation Binary Sequences: On Improved Merit Factors and Runtime Predictions to Achieve Them

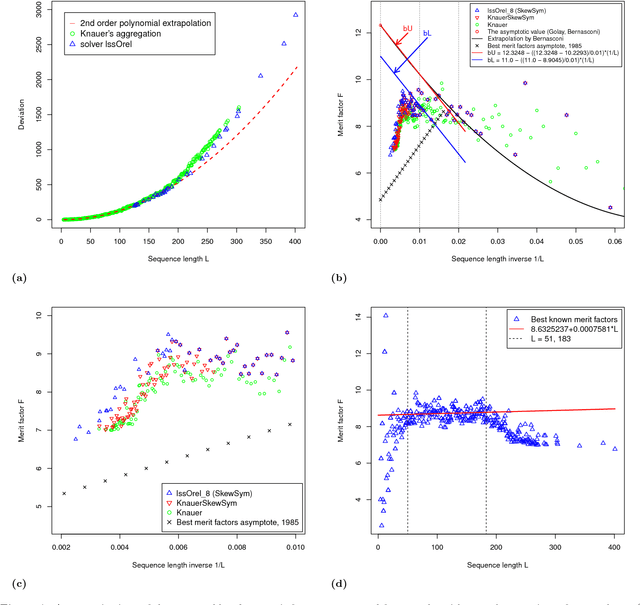
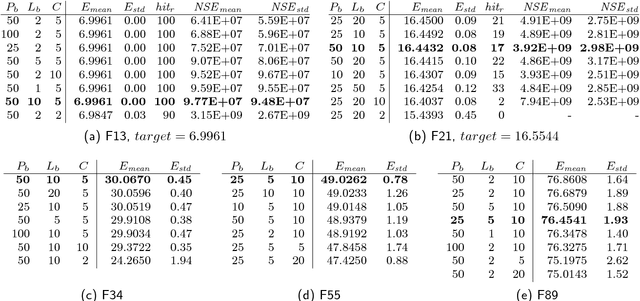
The search for binary sequences with a high figure of merit, known as the low autocorrelation binary sequence ($labs$}) problem, represents a formidable computational challenge. To mitigate the computational constraints of the problem, we consider solvers that accept odd values of sequence length $L$ and return solutions for skew-symmetric binary sequences only -- with the consequence that not all best solutions under this constraint will be optimal for each $L$. In order to improve both, the search for best merit factor $and$ the asymptotic runtime performance, we instrumented three stochastic solvers, the first two are state-of-the-art solvers that rely on variants of memetic and tabu search ($lssMAts$ and $lssRRts$), the third solver ($lssOrel$) organizes the search as a sequence of independent contiguous self-avoiding walk segments. By adapting a rigorous statistical methodology to performance testing of all three combinatorial solvers, experiments show that the solver with the best asymptotic average-case performance, $lssOrel\_8 = 0.000032*1.1504^L$, has the best chance of finding solutions that improve, as $L$ increases, figures of merit reported to date. The same methodology can be applied to engineering new $labs$ solvers that may return merit factors even closer to the conjectured asymptotic value of 12.3248.