Low-Autocorrelation Binary Sequences: On Improved Merit Factors and Runtime Predictions to Achieve Them
Paper and Code
May 06, 2017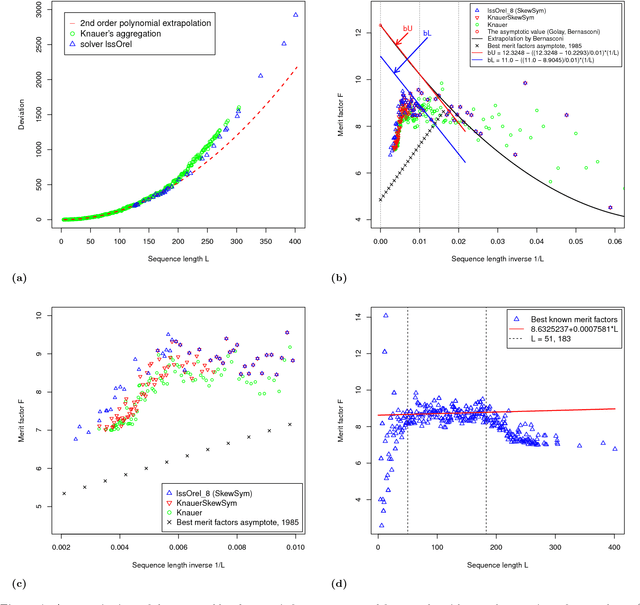

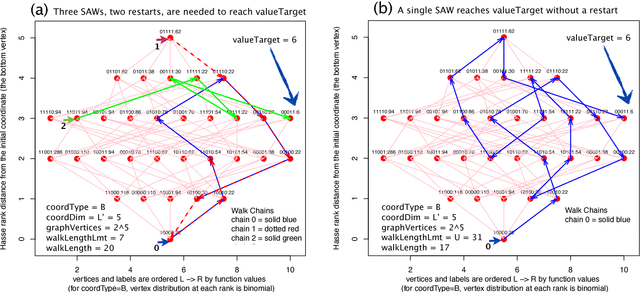
The search for binary sequences with a high figure of merit, known as the low autocorrelation binary sequence ($labs$}) problem, represents a formidable computational challenge. To mitigate the computational constraints of the problem, we consider solvers that accept odd values of sequence length $L$ and return solutions for skew-symmetric binary sequences only -- with the consequence that not all best solutions under this constraint will be optimal for each $L$. In order to improve both, the search for best merit factor $and$ the asymptotic runtime performance, we instrumented three stochastic solvers, the first two are state-of-the-art solvers that rely on variants of memetic and tabu search ($lssMAts$ and $lssRRts$), the third solver ($lssOrel$) organizes the search as a sequence of independent contiguous self-avoiding walk segments. By adapting a rigorous statistical methodology to performance testing of all three combinatorial solvers, experiments show that the solver with the best asymptotic average-case performance, $lssOrel\_8 = 0.000032*1.1504^L$, has the best chance of finding solutions that improve, as $L$ increases, figures of merit reported to date. The same methodology can be applied to engineering new $labs$ solvers that may return merit factors even closer to the conjectured asymptotic value of 12.3248.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge