Graph 3-coloring with a hybrid self-adaptive evolutionary algorithm

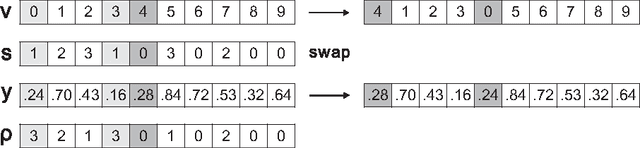
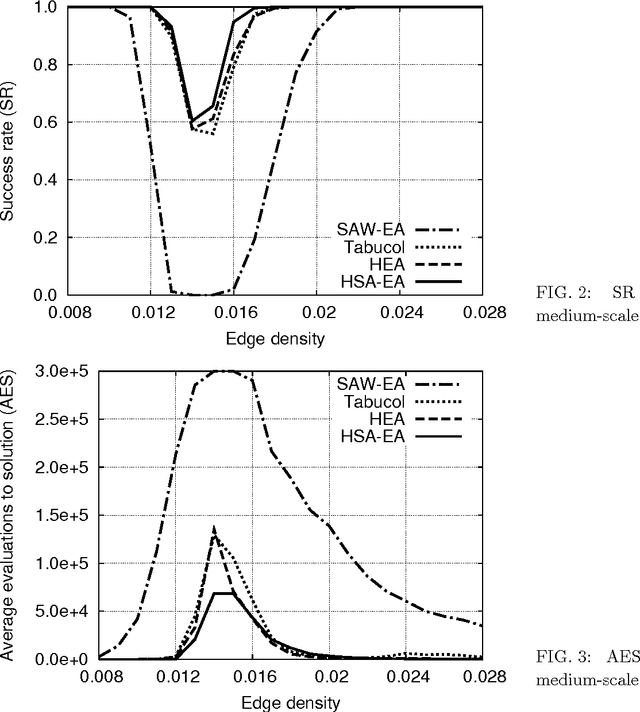
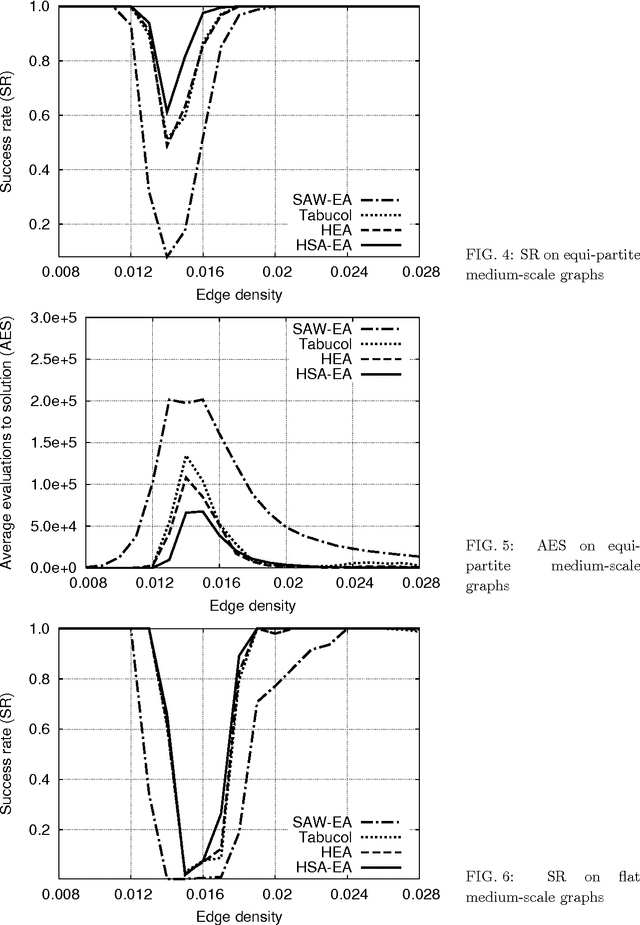
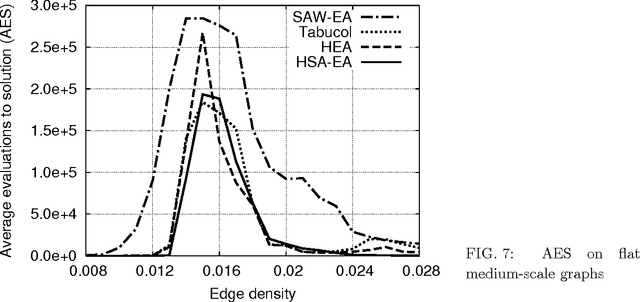
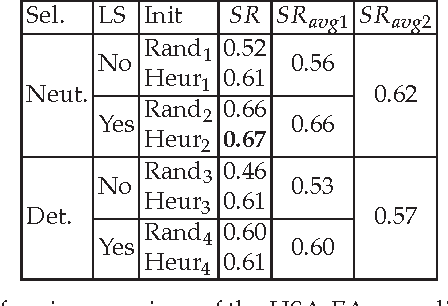
This paper proposes a hybrid self-adaptive evolutionary algorithm for graph coloring that is hybridized with the following novel elements: heuristic genotype-phenotype mapping, a swap local search heuristic, and a neutral survivor selection operator. This algorithm was compared with the evolutionary algorithm with the SAW method of Eiben et al., the Tabucol algorithm of Hertz and de Werra, and the hybrid evolutionary algorithm of Galinier and Hao. The performance of these algorithms were tested on a test suite consisting of randomly generated 3-colorable graphs of various structural features, such as graph size, type, edge density, and variability in sizes of color classes. Furthermore, the test graphs were generated including the phase transition where the graphs are hard to color. The purpose of the extensive experimental work was threefold: to investigate the behavior of the tested algorithms in the phase transition, to identify what impact hybridization with the DSatur traditional heuristic has on the evolutionary algorithm, and to show how graph structural features influence the performance of the graph-coloring algorithms. The results indicate that the performance of the hybrid self-adaptive evolutionary algorithm is comparable with, or better than, the performance of the hybrid evolutionary algorithm which is one of the best graph-coloring algorithms today. Moreover, the fact that all the considered algorithms performed poorly on flat graphs confirms that this type of graphs is really the hardest to color.

Hybridization of Evolutionary Algorithms

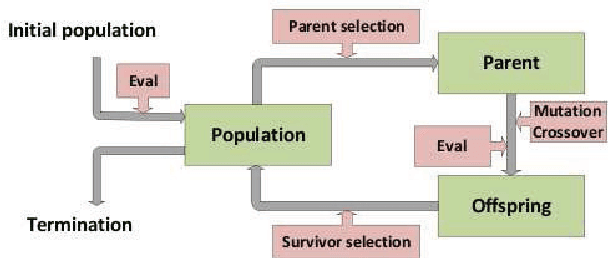
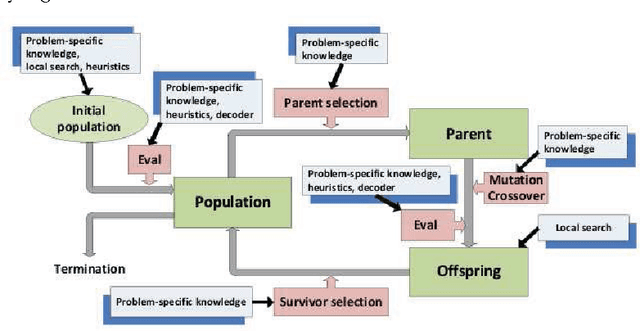
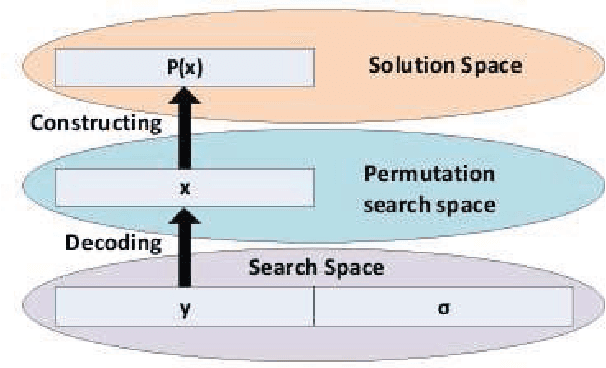
Evolutionary algorithms are good general problem solver but suffer from a lack of domain specific knowledge. However, the problem specific knowledge can be added to evolutionary algorithms by hybridizing. Interestingly, all the elements of the evolutionary algorithms can be hybridized. In this chapter, the hybridization of the three elements of the evolutionary algorithms is discussed: the objective function, the survivor selection operator and the parameter settings. As an objective function, the existing heuristic function that construct the solution of the problem in traditional way is used. However, this function is embedded into the evolutionary algorithm that serves as a generator of new solutions. In addition, the objective function is improved by local search heuristics. The new neutral selection operator has been developed that is capable to deal with neutral solutions, i.e. solutions that have the different representation but expose the equal values of objective function. The aim of this operator is to directs the evolutionary search into a new undiscovered regions of the search space. To avoid of wrong setting of parameters that control the behavior of the evolutionary algorithm, the self-adaptation is used. Finally, such hybrid self-adaptive evolutionary algorithm is applied to the two real-world NP-hard problems: the graph 3-coloring and the optimization of markers in the clothing industry. Extensive experiments shown that these hybridization improves the results of the evolutionary algorithms a lot. Furthermore, the impact of the particular hybridizations is analyzed in details as well.