Conditional Neural Style Transfer with Peer-Regularized Feature Transform

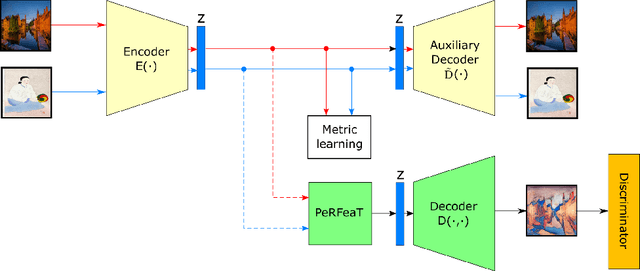
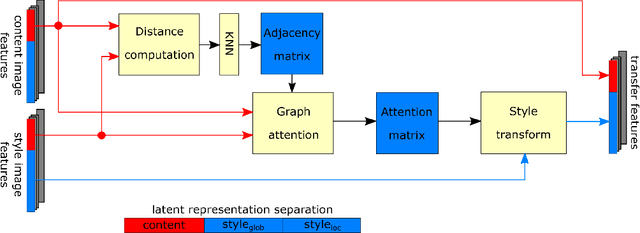
This paper introduces a neural style transfer model to conditionally generate a stylized image using only a set of examples describing the desired style. The proposed solution produces high-quality images even in the zero-shot setting and allows for greater freedom in changing the content geometry. This is thanks to the introduction of a novel Peer-Regularization Layer that recomposes style in latent space by means of a custom graph convolutional layer aiming at separating style and content. Contrary to the vast majority of existing solutions our model does not require any pre-trained network for computing perceptual losses and can be trained fully end-to-end with a new set of cyclic losses that operate directly in latent space. An extensive ablation study confirms the usefulness of the proposed losses and of the Peer-Regularization Layer, with qualitative results that are competitive with respect to the current state-of-the-art even in the challenging zero-shot setting. This opens the door to more abstract and artistic neural image generation scenarios and easier deployment of the model in. production

PeerNets: Exploiting Peer Wisdom Against Adversarial Attacks

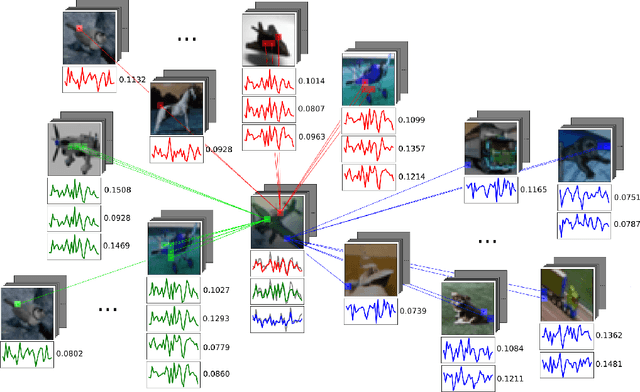
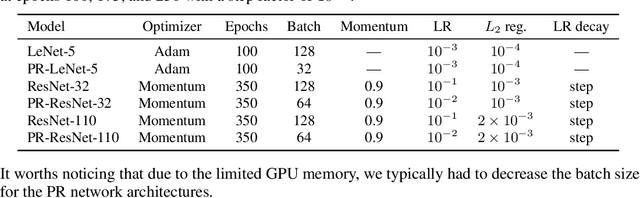
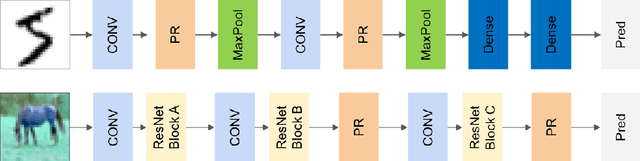
Deep learning systems have become ubiquitous in many aspects of our lives. Unfortunately, it has been shown that such systems are vulnerable to adversarial attacks, making them prone to potential unlawful uses. Designing deep neural networks that are robust to adversarial attacks is a fundamental step in making such systems safer and deployable in a broader variety of applications (e.g. autonomous driving), but more importantly is a necessary step to design novel and more advanced architectures built on new computational paradigms rather than marginally building on the existing ones. In this paper we introduce PeerNets, a novel family of convolutional networks alternating classical Euclidean convolutions with graph convolutions to harness information from a graph of peer samples. This results in a form of non-local forward propagation in the model, where latent features are conditioned on the global structure induced by the graph, that is up to 3 times more robust to a variety of white- and black-box adversarial attacks compared to conventional architectures with almost no drop in accuracy.

Generative Convolutional Networks for Latent Fingerprint Reconstruction

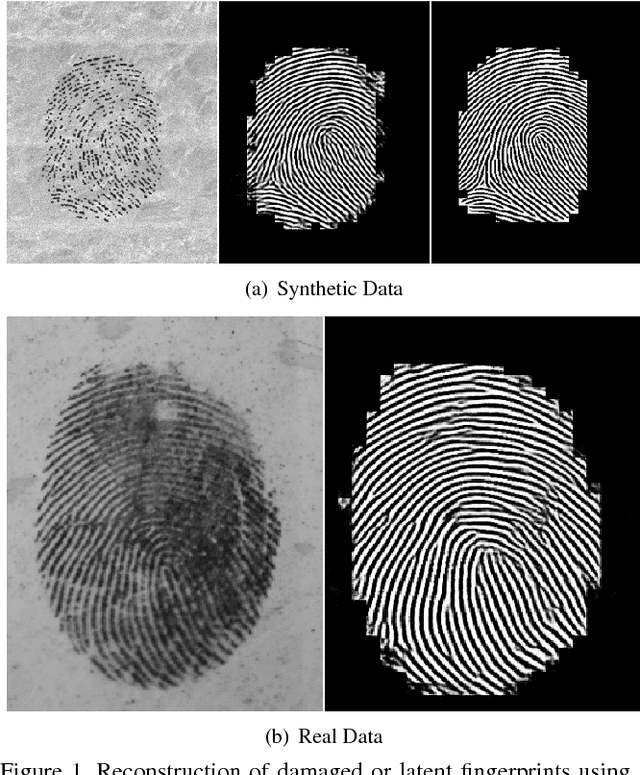
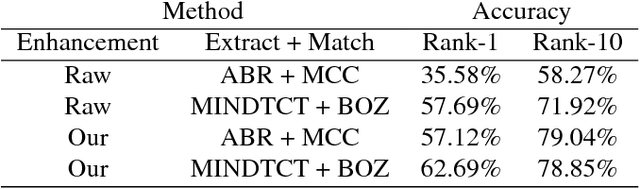
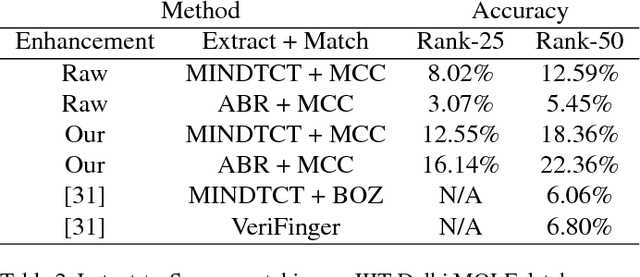
Performance of fingerprint recognition depends heavily on the extraction of minutiae points. Enhancement of the fingerprint ridge pattern is thus an essential pre-processing step that noticeably reduces false positive and negative detection rates. A particularly challenging setting is when the fingerprint images are corrupted or partially missing. In this work, we apply generative convolutional networks to denoise visible minutiae and predict the missing parts of the ridge pattern. The proposed enhancement approach is tested as a pre-processing step in combination with several standard feature extraction methods such as MINDTCT, followed by biometric comparison using MCC and BOZORTH3. We evaluate our method on several publicly available latent fingerprint datasets captured using different sensors.

Geometric deep learning on graphs and manifolds using mixture model CNNs

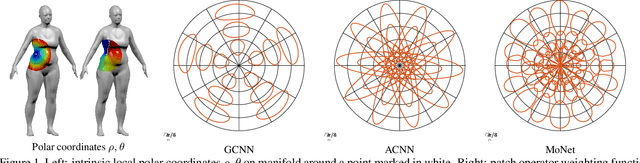
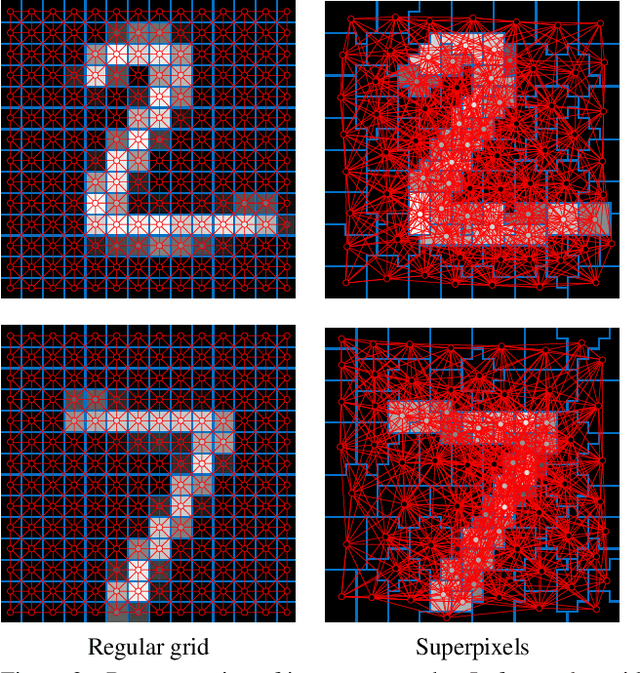
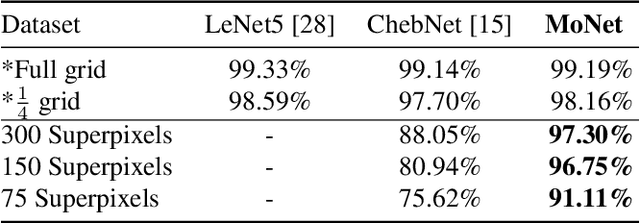
Deep learning has achieved a remarkable performance breakthrough in several fields, most notably in speech recognition, natural language processing, and computer vision. In particular, convolutional neural network (CNN) architectures currently produce state-of-the-art performance on a variety of image analysis tasks such as object detection and recognition. Most of deep learning research has so far focused on dealing with 1D, 2D, or 3D Euclidean-structured data such as acoustic signals, images, or videos. Recently, there has been an increasing interest in geometric deep learning, attempting to generalize deep learning methods to non-Euclidean structured data such as graphs and manifolds, with a variety of applications from the domains of network analysis, computational social science, or computer graphics. In this paper, we propose a unified framework allowing to generalize CNN architectures to non-Euclidean domains (graphs and manifolds) and learn local, stationary, and compositional task-specific features. We show that various non-Euclidean CNN methods previously proposed in the literature can be considered as particular instances of our framework. We test the proposed method on standard tasks from the realms of image-, graph- and 3D shape analysis and show that it consistently outperforms previous approaches.