Multi-vehicle Dynamic Water Surface Monitoring

Repeated exploration of a water surface to detect objects of interest and their subsequent monitoring is important in search-and-rescue or ocean clean-up operations. Since the location of any detected object is dynamic, we propose to address the combined surface exploration and monitoring of the detected objects by modeling spatio-temporal reward states and coordinating a team of vehicles to collect the rewards. The model characterizes the dynamics of the water surface and enables the planner to predict future system states. The state reward value relevant to the particular water surface cell increases over time and is nullified by being in a sensor range of a vehicle. Thus, the proposed multi-vehicle planning approach is to minimize the collective value of the dynamic model reward states. The purpose is to address vehicles' motion constraints by using model predictive control on receding horizon, thus fully exploiting the utilized vehicles' motion capabilities. Based on the evaluation results, the approach indicates improvement in a solution to the kinematic orienteering problem and the team orienteering problem in the monitoring task compared to the existing solutions. The proposed approach has been experimentally verified, supporting its feasibility in real-world monitoring tasks.

Vehicle Fault-Tolerant Robust Power Transmission Line Inspection Planning

This paper concerns fault-tolerant power transmission line inspection planning as a generalization of the multiple traveling salesmen problem. The addressed inspection planning problem is formulated as a single-depot multiple-vehicle scenario, where the inspection vehicles are constrained by the battery budget limiting their inspection time. The inspection vehicle is assumed to be an autonomous multi-copter with a wide range of possible flight speeds influencing battery consumption. The inspection plan is represented by multiple routes for vehicles providing full coverage over inspection target power lines. On an inspection vehicle mission interruption, which might happen at any time during the execution of the inspection plan, the inspection is re-planned using the remaining vehicles and their remaining battery budgets. Robustness is introduced by choosing a suitable cost function for the initial plan that maximizes the time window for successful re-planning. It enables the remaining vehicles to successfully finish all the inspection targets using their respective remaining battery budgets. A combinatorial metaheuristic algorithm with various cost functions is used for planning and fast re-planning during the inspection.

Multi-Tour Set Traveling Salesman Problem in Planning Power Transmission Line Inspection

This letter concerns optimal power transmission line inspection formulated as a proposed generalization of the traveling salesman problem for a multi-route one-depot scenario. The problem is formulated for an inspection vehicle with a limited travel budget. Therefore, the solution can be composed of multiple runs to provide full coverage of the given power lines. Besides, the solution indicates how many vehicles can perform the inspection in a single run. The optimal solution of the problem is solved by the proposed Integer Linear Programming (ILP) formulation, which is, however, very computationally demanding. Therefore, the computational requirements are addressed by the combinatorial metaheuristic. The employed greedy randomized adaptive search procedure is significantly less demanding while providing competitive solutions and scales better with the problem size than the ILP-based approach. The proposed formulation and algorithms are demonstrated in a real-world scenario to inspect power line segments at the electrical substation.

T*$\varepsilon$ -- Bounded-Suboptimal Efficient Motion Planning for Minimum-Time Planar Curvature-Constrained Systems

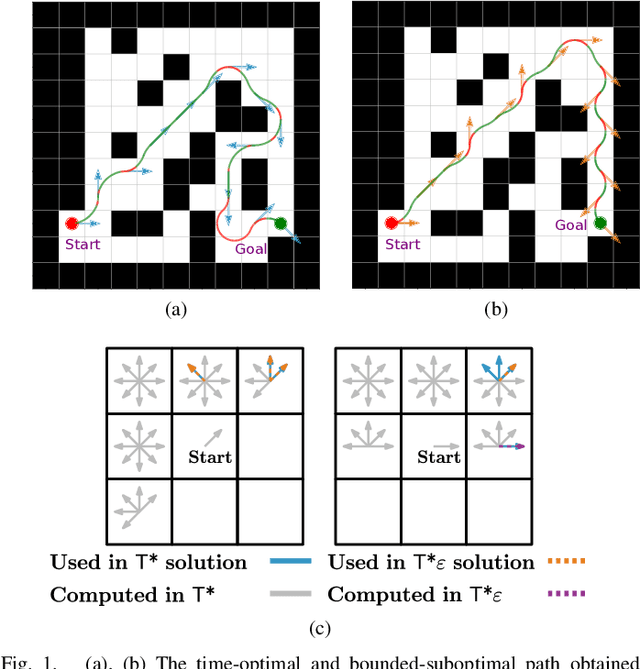
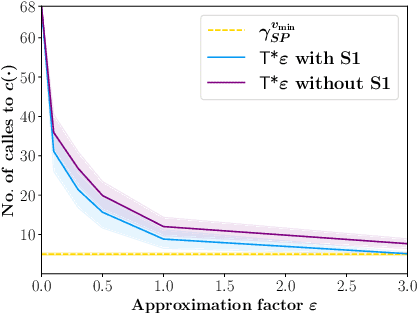
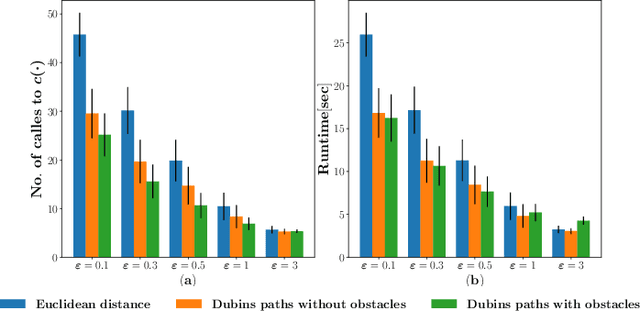
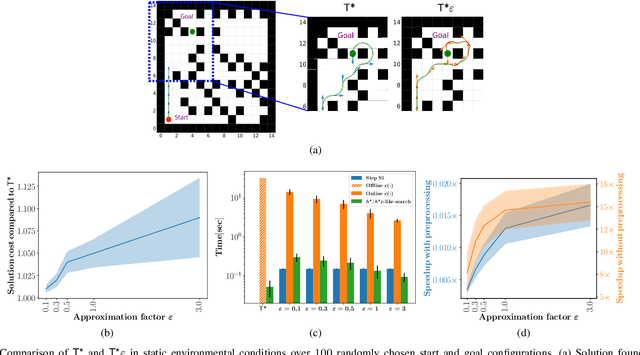
We consider the problem of finding collision-free paths for curvature-constrained systems in the presence of obstacles while minimizing execution time. Specifically, we focus on the setting where a planar system can travel at some range of speeds with unbounded acceleration. This setting can model many systems, such as fixed-wing drones. Unfortunately, planning for such systems might require evaluating many (local) time-optimal transitions connecting two close-by configurations, which is computationally expensive. Existing methods either pre-compute all such transitions in a preprocessing stage or use heuristics to speed up the search, thus foregoing any guarantees on solution quality. Our key insight is that computing all the time-optimal transitions is both~(i)~computationally expensive and~(ii)~unnecessary for many problem instances. We show that by finding bounded-suboptimal solutions (solutions whose cost is bounded by $1+\varepsilon$ times the cost of the optimal solution for any user-provided $\varepsilon$) and not time-optimal solutions, one can dramatically reduce the number of time-optimal transitions used. We demonstrate using empirical evaluation that our planning framework can reduce the runtime by several orders of magnitude compared to the state-of-the-art while still providing guarantees on the quality of the solution.

System for multi-robotic exploration of underground environments CTU-CRAS-NORLAB in the DARPA Subterranean Challenge

We present a field report of CTU-CRAS-NORLAB team from the Subterranean Challenge (SubT) organised by the Defense Advanced Research Projects Agency (DARPA). The contest seeks to advance technologies that would improve the safety and efficiency of search-and-rescue operations in GPS-denied environments. During the contest rounds, teams of mobile robots have to find specific objects while operating in environments with limited radio communication, e.g. mining tunnels, underground stations or natural caverns. We present a heterogeneous exploration robotic system of the CTU-CRAS-NORLAB team, which achieved the third rank at the SubT Tunnel and Urban Circuit rounds and surpassed the performance of all other non-DARPA-funded teams. The field report describes the team's hardware, sensors, algorithms and strategies, and discusses the lessons learned by participating at the DARPA SubT contest.

WiSM: Windowing Surrogate Model for Evaluation of Curvature-Constrained Tours with Dubins vehicle

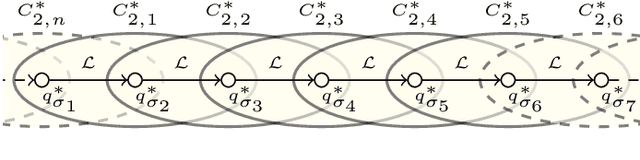
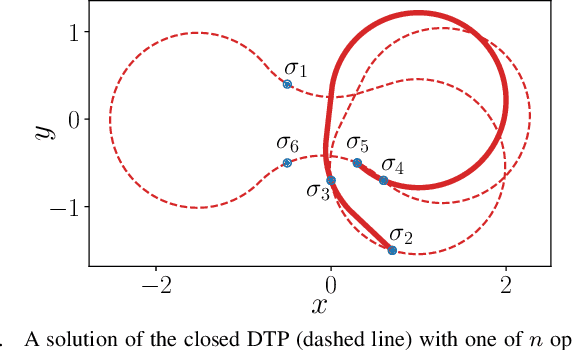
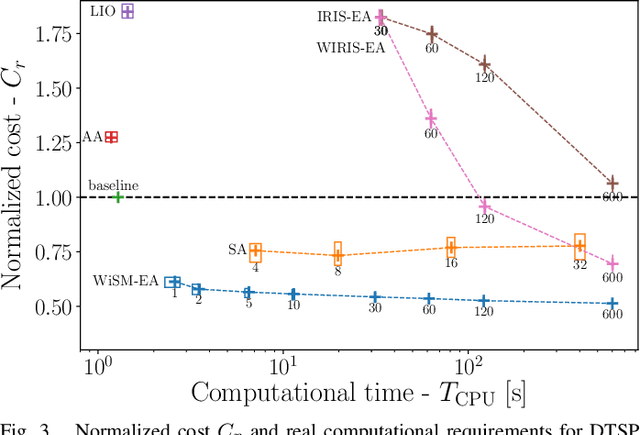
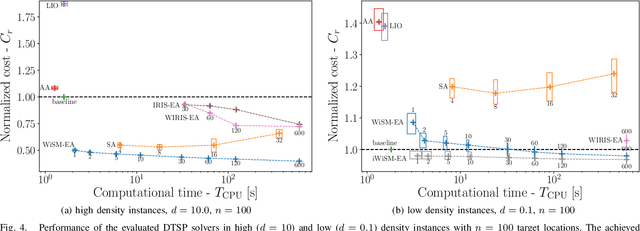
Dubins tours represent a solution of the Dubins Traveling Salesman Problem (DTSP) that is a variant of the optimization routing problem to determine a curvature-constrained shortest path to visit a set of locations such that the path is feasible for Dubins vehicle, which moves only forward and has a limited turning radius. The DTSP combines the NP-hard combinatorial optimization to determine the optimal sequence of visits to the locations, as in the regular TSP, with the continuous optimization of the heading angles at the locations, where the optimal heading values depend on the sequence of visits and vice versa. We address the computationally challenging DTSP by fast evaluation of the sequence of visits by the proposed Windowing Surrogate Model (WiSM) which estimates the length of the optimal Dubins path connecting a sequence of locations in a Dubins tour. The estimation is sped up by a regression model trained using close to optimum solutions of small Dubins tours that are generalized for large-scale instances of the addressed DTSP utilizing the sliding window technique and a cache for already computed results. The reported results support that the proposed WiSM enables a fast convergence of a relatively simple evolutionary algorithm to high-quality solutions of the DTSP. We show that with an increasing number of locations, our algorithm scales significantly better than other state-of-the-art DTSP solvers.