Doron Pinsky
T*$\varepsilon$ -- Bounded-Suboptimal Efficient Motion Planning for Minimum-Time Planar Curvature-Constrained Systems
Apr 04, 2022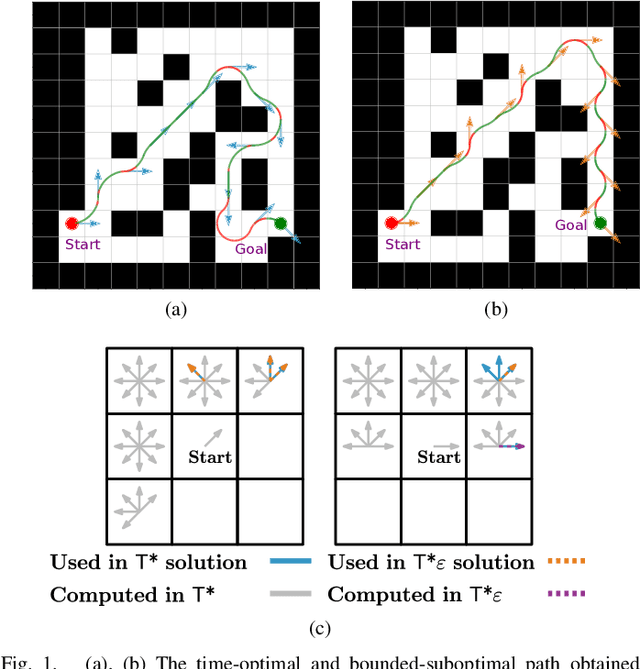
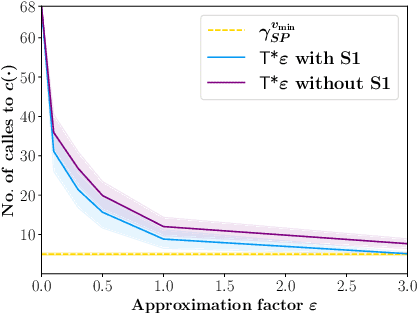
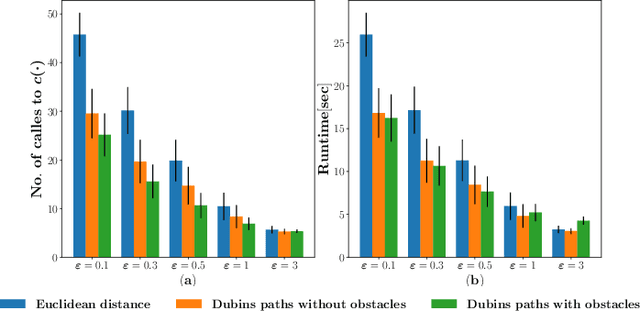
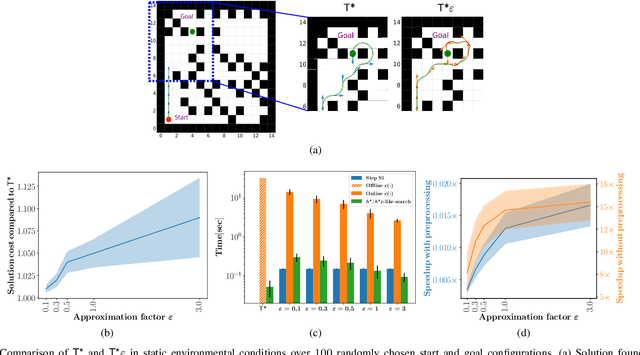
Abstract:We consider the problem of finding collision-free paths for curvature-constrained systems in the presence of obstacles while minimizing execution time. Specifically, we focus on the setting where a planar system can travel at some range of speeds with unbounded acceleration. This setting can model many systems, such as fixed-wing drones. Unfortunately, planning for such systems might require evaluating many (local) time-optimal transitions connecting two close-by configurations, which is computationally expensive. Existing methods either pre-compute all such transitions in a preprocessing stage or use heuristics to speed up the search, thus foregoing any guarantees on solution quality. Our key insight is that computing all the time-optimal transitions is both~(i)~computationally expensive and~(ii)~unnecessary for many problem instances. We show that by finding bounded-suboptimal solutions (solutions whose cost is bounded by $1+\varepsilon$ times the cost of the optimal solution for any user-provided $\varepsilon$) and not time-optimal solutions, one can dramatically reduce the number of time-optimal transitions used. We demonstrate using empirical evaluation that our planning framework can reduce the runtime by several orders of magnitude compared to the state-of-the-art while still providing guarantees on the quality of the solution.
* 8 pages, 6 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge