T*$\varepsilon$ -- Bounded-Suboptimal Efficient Motion Planning for Minimum-Time Planar Curvature-Constrained Systems

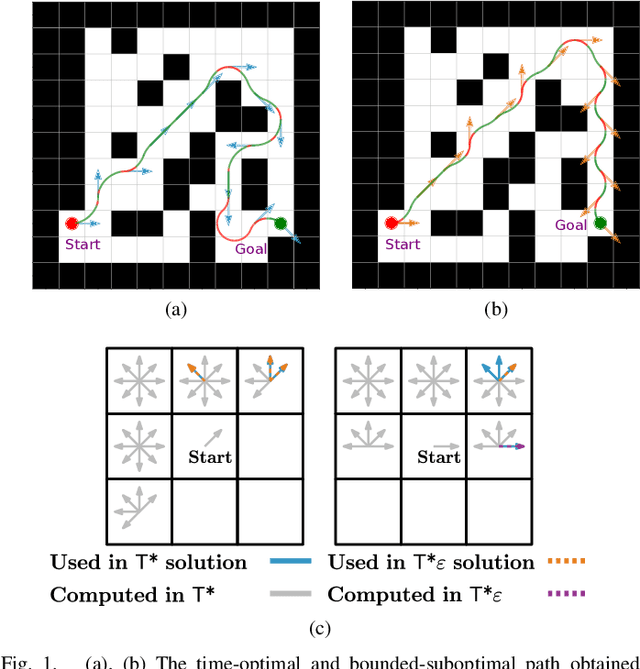
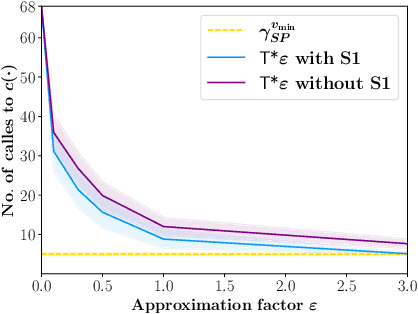
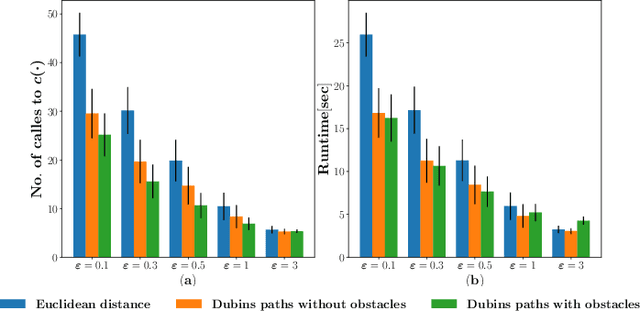
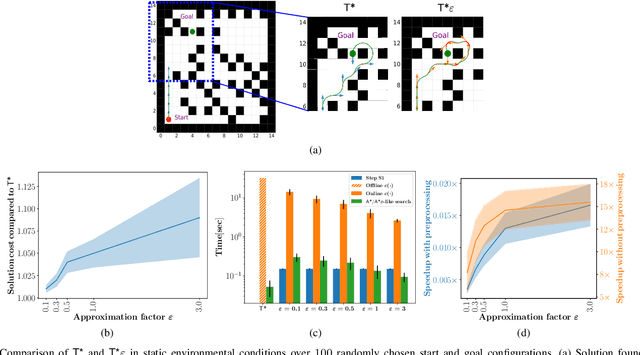
We consider the problem of finding collision-free paths for curvature-constrained systems in the presence of obstacles while minimizing execution time. Specifically, we focus on the setting where a planar system can travel at some range of speeds with unbounded acceleration. This setting can model many systems, such as fixed-wing drones. Unfortunately, planning for such systems might require evaluating many (local) time-optimal transitions connecting two close-by configurations, which is computationally expensive. Existing methods either pre-compute all such transitions in a preprocessing stage or use heuristics to speed up the search, thus foregoing any guarantees on solution quality. Our key insight is that computing all the time-optimal transitions is both~(i)~computationally expensive and~(ii)~unnecessary for many problem instances. We show that by finding bounded-suboptimal solutions (solutions whose cost is bounded by $1+\varepsilon$ times the cost of the optimal solution for any user-provided $\varepsilon$) and not time-optimal solutions, one can dramatically reduce the number of time-optimal transitions used. We demonstrate using empirical evaluation that our planning framework can reduce the runtime by several orders of magnitude compared to the state-of-the-art while still providing guarantees on the quality of the solution.

WiSM: Windowing Surrogate Model for Evaluation of Curvature-Constrained Tours with Dubins vehicle

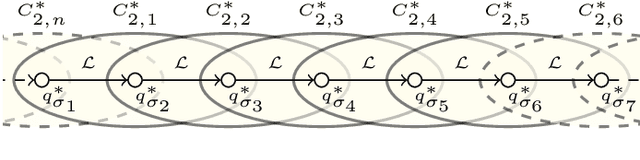
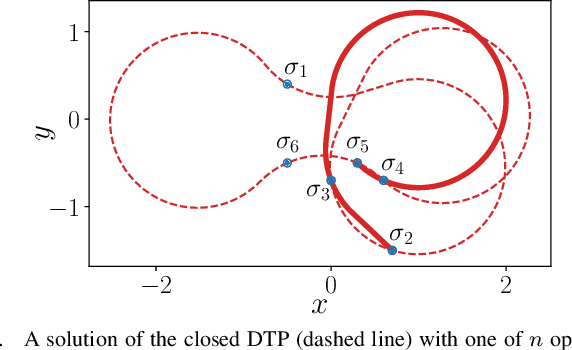
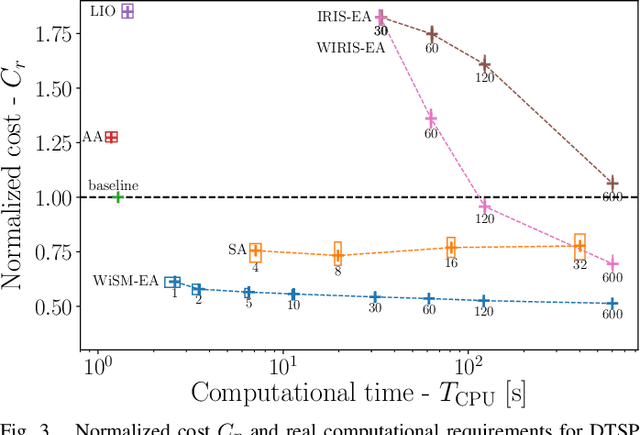
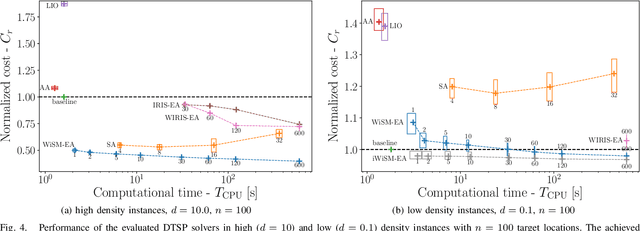
Dubins tours represent a solution of the Dubins Traveling Salesman Problem (DTSP) that is a variant of the optimization routing problem to determine a curvature-constrained shortest path to visit a set of locations such that the path is feasible for Dubins vehicle, which moves only forward and has a limited turning radius. The DTSP combines the NP-hard combinatorial optimization to determine the optimal sequence of visits to the locations, as in the regular TSP, with the continuous optimization of the heading angles at the locations, where the optimal heading values depend on the sequence of visits and vice versa. We address the computationally challenging DTSP by fast evaluation of the sequence of visits by the proposed Windowing Surrogate Model (WiSM) which estimates the length of the optimal Dubins path connecting a sequence of locations in a Dubins tour. The estimation is sped up by a regression model trained using close to optimum solutions of small Dubins tours that are generalized for large-scale instances of the addressed DTSP utilizing the sliding window technique and a cache for already computed results. The reported results support that the proposed WiSM enables a fast convergence of a relatively simple evolutionary algorithm to high-quality solutions of the DTSP. We show that with an increasing number of locations, our algorithm scales significantly better than other state-of-the-art DTSP solvers.