Deep linear neural networks with arbitrary loss: All local minima are global

We consider deep linear networks with arbitrary convex differentiable loss. We provide a short and elementary proof of the fact that all local minima are global minima if the hidden layers are either 1) at least as wide as the input layer, or 2) at least as wide as the output layer. This result is the strongest possible in the following sense: If the loss is convex and Lipschitz but not differentiable then deep linear networks can have sub-optimal local minima.

The Multilinear Structure of ReLU Networks

We study the loss surface of neural networks equipped with a hinge loss criterion and ReLU or leaky ReLU nonlinearities. Any such network defines a piecewise multilinear form in parameter space. By appealing to harmonic analysis we show that all local minima of such network are non-differentiable, except for those minima that occur in a region of parameter space where the loss surface is perfectly flat. Non-differentiable minima are therefore not technicalities or pathologies; they are heart of the problem when investigating the loss of ReLU networks. As a consequence, we must employ techniques from nonsmooth analysis to study these loss surfaces. We show how to apply these techniques in some illustrative cases.

A recurrent neural network without chaos

We introduce an exceptionally simple gated recurrent neural network (RNN) that achieves performance comparable to well-known gated architectures, such as LSTMs and GRUs, on the word-level language modeling task. We prove that our model has simple, predicable and non-chaotic dynamics. This stands in stark contrast to more standard gated architectures, whose underlying dynamical systems exhibit chaotic behavior.

Enhanced Lasso Recovery on Graph

This work aims at recovering signals that are sparse on graphs. Compressed sensing offers techniques for signal recovery from a few linear measurements and graph Fourier analysis provides a signal representation on graph. In this paper, we leverage these two frameworks to introduce a new Lasso recovery algorithm on graphs. More precisely, we present a non-convex, non-smooth algorithm that outperforms the standard convex Lasso technique. We carry out numerical experiments on three benchmark graph datasets.

Consistency of Cheeger and Ratio Graph Cuts

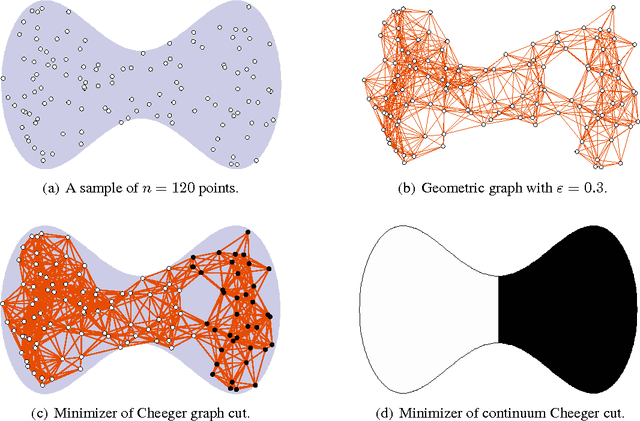
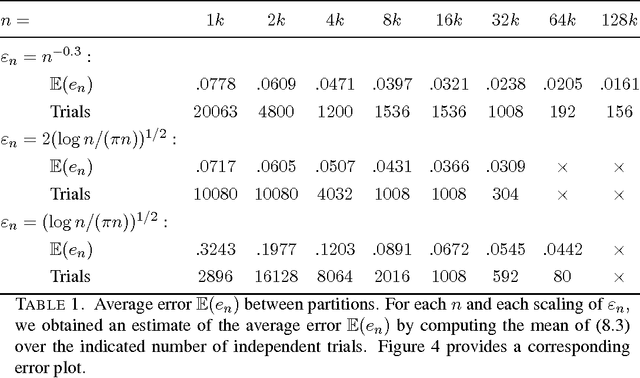
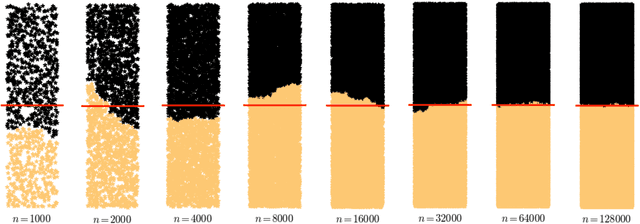
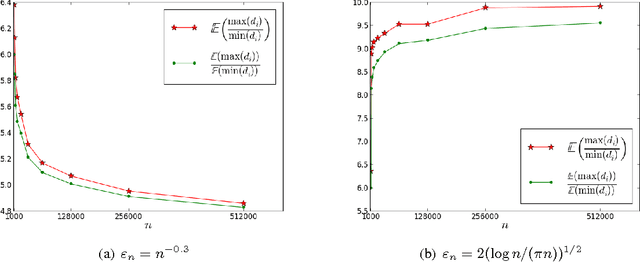
This paper establishes the consistency of a family of graph-cut-based algorithms for clustering of data clouds. We consider point clouds obtained as samples of a ground-truth measure. We investigate approaches to clustering based on minimizing objective functionals defined on proximity graphs of the given sample. Our focus is on functionals based on graph cuts like the Cheeger and ratio cuts. We show that minimizers of the these cuts converge as the sample size increases to a minimizer of a corresponding continuum cut (which partitions the ground truth measure). Moreover, we obtain sharp conditions on how the connectivity radius can be scaled with respect to the number of sample points for the consistency to hold. We provide results for two-way and for multiway cuts. Furthermore we provide numerical experiments that illustrate the results and explore the optimality of scaling in dimension two.

An Incremental Reseeding Strategy for Clustering

In this work we propose a simple and easily parallelizable algorithm for multiway graph partitioning. The algorithm alternates between three basic components: diffusing seed vertices over the graph, thresholding the diffused seeds, and then randomly reseeding the thresholded clusters. We demonstrate experimentally that the proper combination of these ingredients leads to an algorithm that achieves state-of-the-art performance in terms of cluster purity on standard benchmarks datasets. Moreover, the algorithm runs an order of magnitude faster than the other algorithms that achieve comparable results in terms of accuracy. We also describe a coarsen, cluster and refine approach similar to GRACLUS and METIS that removes an additional order of magnitude from the runtime of our algorithm while still maintaining competitive accuracy.