Poisson Learning: Graph Based Semi-Supervised Learning At Very Low Label Rates

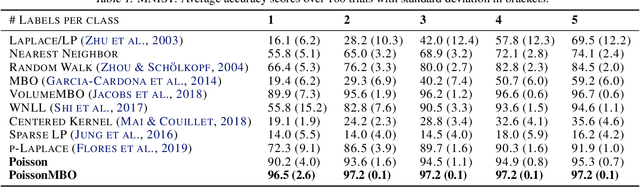
We propose a new framework, called Poisson learning, for graph based semi-supervised learning at very low label rates. Poisson learning is motivated by the need to address the degeneracy of Laplacian semi-supervised learning in this regime. The method replaces the assignment of label values at training points with the placement of sources and sinks, and solves the resulting Poisson equation on the graph. The outcomes are provably more stable and informative than those of Laplacian learning. Poisson learning is efficient and simple to implement, and we present numerical experiments showing the method is superior to other recent approaches to semi-supervised learning at low label rates on MNIST, FashionMNIST, and Cifar-10. We also propose a graph-cut enhancement of Poisson learning, called Poisson MBO, that gives higher accuracy and can incorporate prior knowledge of relative class sizes.

Properly-weighted graph Laplacian for semi-supervised learning

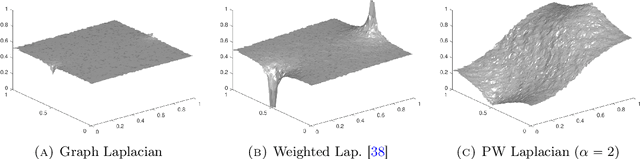
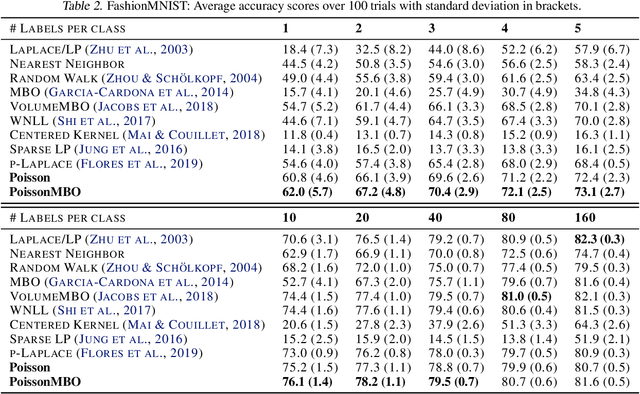
The performance of traditional graph Laplacian methods for semi-supervised learning degrades substantially as the ratio of labeled to unlabeled data decreases, due to a degeneracy in the graph Laplacian. Several approaches have been proposed recently to address this, however we show that some of them remain ill-posed in the large-data limit. In this paper, we show a way to correctly set the weights in Laplacian regularization so that the estimator remains well posed and stable in the large-sample limit. We prove that our semi-supervised learning algorithm converges, in the infinite sample size limit, to the smooth solution of a continuum variational problem that attains the labeled values continuously. Our method is fast and easy to implement.

Error estimates for spectral convergence of the graph Laplacian on random geometric graphs towards the Laplace--Beltrami operator

We study the convergence of the graph Laplacian of a random geometric graph generated by an i.i.d. sample from a $m$-dimensional submanifold $M$ in $R^d$ as the sample size $n$ increases and the neighborhood size $h$ tends to zero. We show that eigenvalues and eigenvectors of the graph Laplacian converge with a rate of $O\Big(\big(\frac{\log n}{n}\big)^\frac{1}{2m}\Big)$ to the eigenvalues and eigenfunctions of the weighted Laplace-Beltrami operator of $M$. No information on the submanifold $M$ is needed in the construction of the graph or the "out-of-sample extension" of the eigenvectors. Of independent interest is a generalization of the rate of convergence of empirical measures on submanifolds in $R^d$ in infinity transportation distance.

Consistency of Cheeger and Ratio Graph Cuts

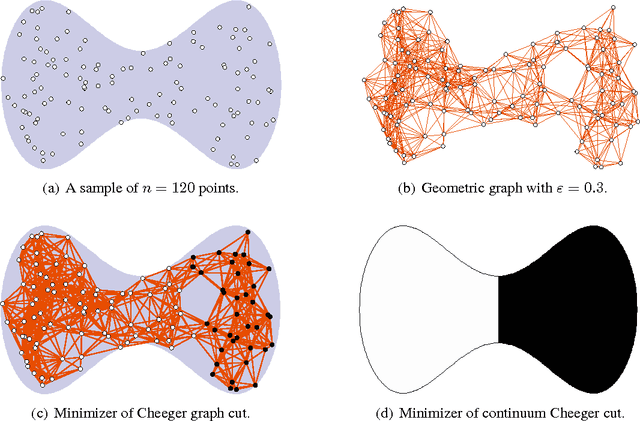
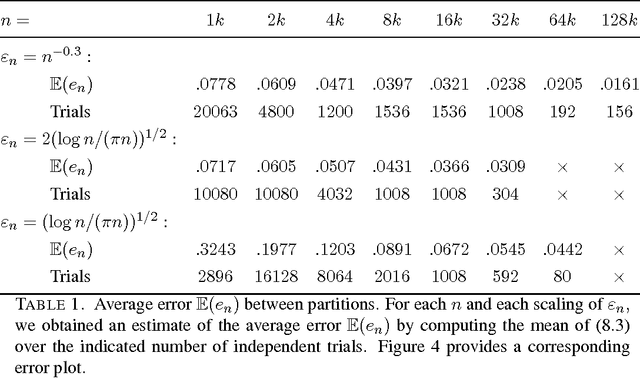
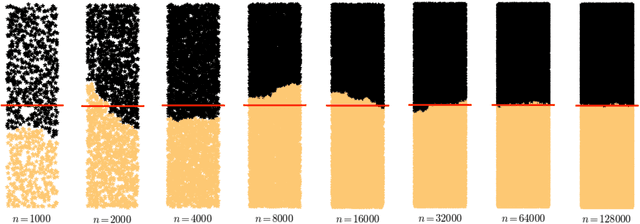
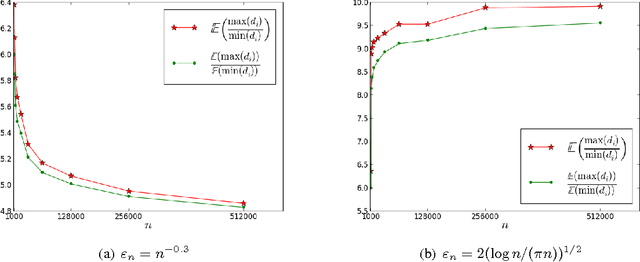
This paper establishes the consistency of a family of graph-cut-based algorithms for clustering of data clouds. We consider point clouds obtained as samples of a ground-truth measure. We investigate approaches to clustering based on minimizing objective functionals defined on proximity graphs of the given sample. Our focus is on functionals based on graph cuts like the Cheeger and ratio cuts. We show that minimizers of the these cuts converge as the sample size increases to a minimizer of a corresponding continuum cut (which partitions the ground truth measure). Moreover, we obtain sharp conditions on how the connectivity radius can be scaled with respect to the number of sample points for the consistency to hold. We provide results for two-way and for multiway cuts. Furthermore we provide numerical experiments that illustrate the results and explore the optimality of scaling in dimension two.