Learning Algorithms for Intelligent Agents and Mechanisms

In this thesis, we research learning algorithms for optimal decision making in two different contexts, Reinforcement Learning in Part I and Auction Design in Part II. Reinforcement learning (RL) is an area of machine learning that is concerned with how an agent should act in an environment in order to maximize its cumulative reward over time. In Chapter 2, inspired by statistical physics, we develop a novel approach to Reinforcement Learning (RL) that not only learns optimal policies with enhanced desirable properties but also sheds new light on maximum entropy RL. In Chapter 3, we tackle the generalization problem in RL using a Bayesian perspective. We show that imperfect knowledge of the environments dynamics effectively turn a fully-observed Markov Decision Process (MDP) into a Partially Observed MDP (POMDP) that we call the Epistemic POMDP. Informed by this observation, we develop a new policy learning algorithm LEEP which has improved generalization properties. Designing an incentive compatible, individually rational auction that maximizes revenue is a challenging and intractable problem. Recently, deep learning based approaches have been proposed to learn optimal auctions from data. While successful, this approach suffers from a few limitations, including sample inefficiency, lack of generalization to new auctions, and training difficulties. In Chapter 4, we construct a symmetry preserving neural network architecture, EquivariantNet, suitable for anonymous auctions. EquivariantNet is not only more sample efficient but is also able to learn auction rules that generalize well to other settings. In Chapter 5, we propose a novel formulation of the auction learning problem as a two player game. The resulting learning algorithm, ALGNet, is easier to train, more reliable and better suited for non stationary settings.

Why Generalization in RL is Difficult: Epistemic POMDPs and Implicit Partial Observability

Generalization is a central challenge for the deployment of reinforcement learning (RL) systems in the real world. In this paper, we show that the sequential structure of the RL problem necessitates new approaches to generalization beyond the well-studied techniques used in supervised learning. While supervised learning methods can generalize effectively without explicitly accounting for epistemic uncertainty, we show that, perhaps surprisingly, this is not the case in RL. We show that generalization to unseen test conditions from a limited number of training conditions induces implicit partial observability, effectively turning even fully-observed MDPs into POMDPs. Informed by this observation, we recast the problem of generalization in RL as solving the induced partially observed Markov decision process, which we call the epistemic POMDP. We demonstrate the failure modes of algorithms that do not appropriately handle this partial observability, and suggest a simple ensemble-based technique for approximately solving the partially observed problem. Empirically, we demonstrate that our simple algorithm derived from the epistemic POMDP achieves significant gains in generalization over current methods on the Procgen benchmark suite.

Auction learning as a two-player game

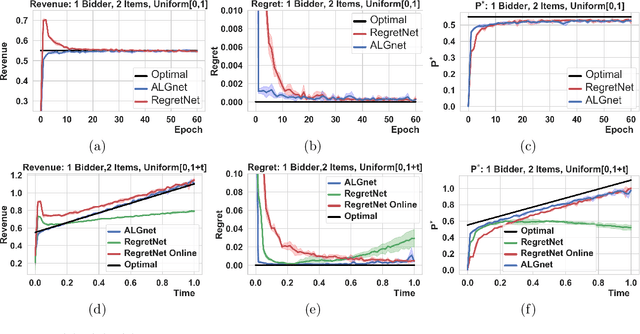
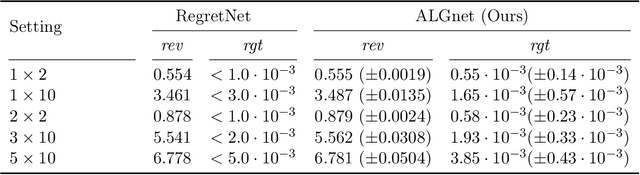
Designing an incentive compatible auction that maximizes expected revenue is a central problem in Auction Design. While theoretical approaches to the problem have hit some limits, a recent research direction initiated by Duetting et al. (2019) consists in building neural network architectures to find optimal auctions. We propose two conceptual deviations from their approach which result in enhanced performance. First, we use recent results in theoretical auction design (Rubinstein and Weinberg, 2018) to introduce a time-independent Lagrangian. This not only circumvents the need for an expensive hyper-parameter search (as in prior work), but also provides a principled metric to compare the performance of two auctions (absent from prior work). Second, the optimization procedure in previous work uses an inner maximization loop to compute optimal misreports. We amortize this process through the introduction of an additional neural network. We demonstrate the effectiveness of our approach by learning competitive or strictly improved auctions compared to prior work. Both results together further imply a novel formulation of Auction Design as a two-player game with stationary utility functions.

A Permutation-Equivariant Neural Network Architecture For Auction Design

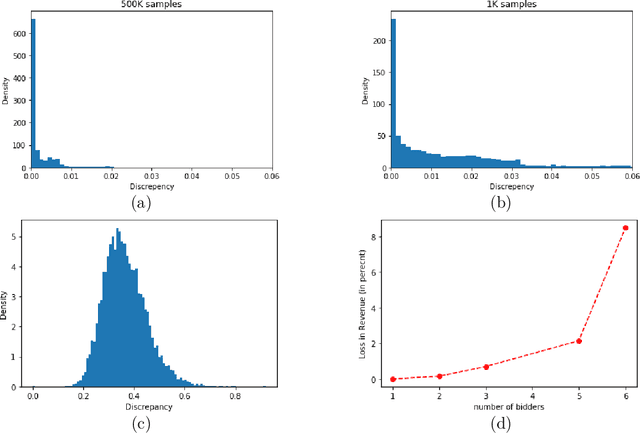
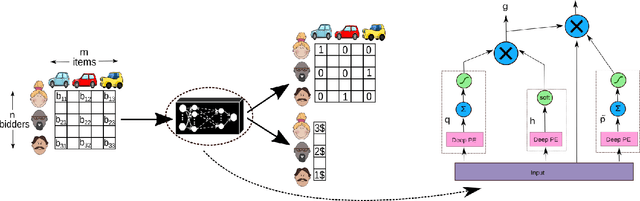
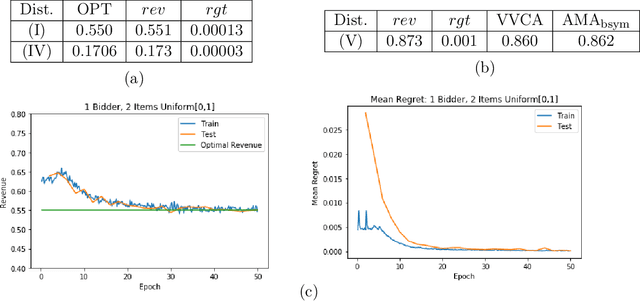
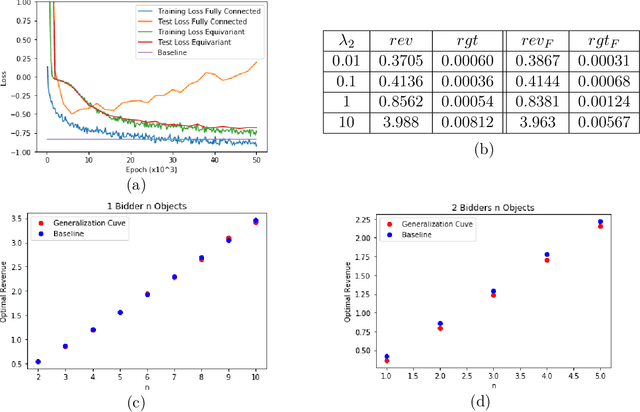
Designing an incentive compatible auction that maximizes expected revenue is a central problem in Auction Design. Theoretical approaches to the problem have hit some limits in the past decades and analytical solutions are known for only a few simple settings. Computational approaches to the problem through the use of LPs have their own set of limitations. Building on the success of deep learning, a new approach was recently proposed by D\"utting et al., 2017 in which the auction is modeled by a feed-forward neural network and the design problem is framed as a learning problem. The neural architectures used in that work are general purpose and do not take advantage of any of the symmetries the problem could present, such as permutation equivariance. In this work, we consider auction design problems that have permutation-equivariant symmetry and construct a neural architecture that is capable of perfectly recovering the permutation-equivariant optimal mechanism, which we show is not possible with the previous architecture. We demonstrate that permutation-equivariant architectures are not only capable of recovering previous results, they also have better generalization properties.

A Theoretical Connection Between Statistical Physics and Reinforcement Learning

Sequential decision making in the presence of uncertainty and stochastic dynamics gives rise to distributions over state/action trajectories in reinforcement learning (RL) and optimal control problems. This observation has led to a variety of connections between RL and inference in probabilistic graphical models (PGMs). Here we explore a different dimension to this relationship, examining reinforcement learning using the tools and abstractions of statistical physics. The central object in the statistical physics abstraction is the idea of a partition function $\mathcal{Z}$, and here we construct a partition function from the ensemble of possible trajectories that an agent might take in a Markov decision process. Although value functions and $Q$-functions can be derived from this partition function and interpreted via average energies, the $\mathcal{Z}$-function provides an object with its own Bellman equation that can form the basis of alternative dynamic programming approaches. Moreover, when the MDP dynamics are deterministic, the Bellman equation for $\mathcal{Z}$ is linear, allowing direct solutions that are unavailable for the nonlinear equations associated with traditional value functions. The policies learned via these $\mathcal{Z}$-based Bellman updates are tightly linked to Boltzmann-like policy parameterizations. In addition to sampling actions proportionally to the exponential of the expected cumulative reward as Boltzmann policies would, these policies take entropy into account favoring states from which many outcomes are possible.