Learning Algorithms for Intelligent Agents and Mechanisms
Paper and Code
Oct 06, 2022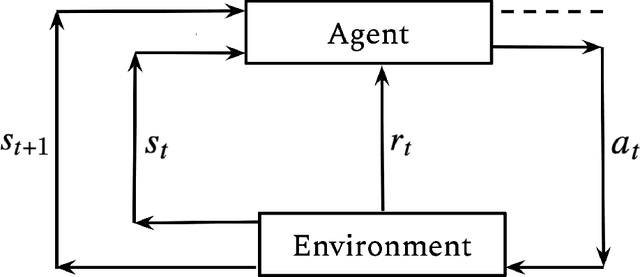

In this thesis, we research learning algorithms for optimal decision making in two different contexts, Reinforcement Learning in Part I and Auction Design in Part II. Reinforcement learning (RL) is an area of machine learning that is concerned with how an agent should act in an environment in order to maximize its cumulative reward over time. In Chapter 2, inspired by statistical physics, we develop a novel approach to Reinforcement Learning (RL) that not only learns optimal policies with enhanced desirable properties but also sheds new light on maximum entropy RL. In Chapter 3, we tackle the generalization problem in RL using a Bayesian perspective. We show that imperfect knowledge of the environments dynamics effectively turn a fully-observed Markov Decision Process (MDP) into a Partially Observed MDP (POMDP) that we call the Epistemic POMDP. Informed by this observation, we develop a new policy learning algorithm LEEP which has improved generalization properties. Designing an incentive compatible, individually rational auction that maximizes revenue is a challenging and intractable problem. Recently, deep learning based approaches have been proposed to learn optimal auctions from data. While successful, this approach suffers from a few limitations, including sample inefficiency, lack of generalization to new auctions, and training difficulties. In Chapter 4, we construct a symmetry preserving neural network architecture, EquivariantNet, suitable for anonymous auctions. EquivariantNet is not only more sample efficient but is also able to learn auction rules that generalize well to other settings. In Chapter 5, we propose a novel formulation of the auction learning problem as a two player game. The resulting learning algorithm, ALGNet, is easier to train, more reliable and better suited for non stationary settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge