Neural Networks and Chaos: Construction, Evaluation of Chaotic Networks, and Prediction of Chaos with Multilayer Feedforward Networks

Many research works deal with chaotic neural networks for various fields of application. Unfortunately, up to now these networks are usually claimed to be chaotic without any mathematical proof. The purpose of this paper is to establish, based on a rigorous theoretical framework, an equivalence between chaotic iterations according to Devaney and a particular class of neural networks. On the one hand we show how to build such a network, on the other hand we provide a method to check if a neural network is a chaotic one. Finally, the ability of classical feedforward multilayer perceptrons to learn sets of data obtained from a dynamical system is regarded. Various Boolean functions are iterated on finite states. Iterations of some of them are proven to be chaotic as it is defined by Devaney. In that context, important differences occur in the training process, establishing with various neural networks that chaotic behaviors are far more difficult to learn.

Hybrid Genetic Algorithm and Lasso Test Approach for Inferring Well Supported Phylogenetic Trees based on Subsets of Chloroplastic Core Genes

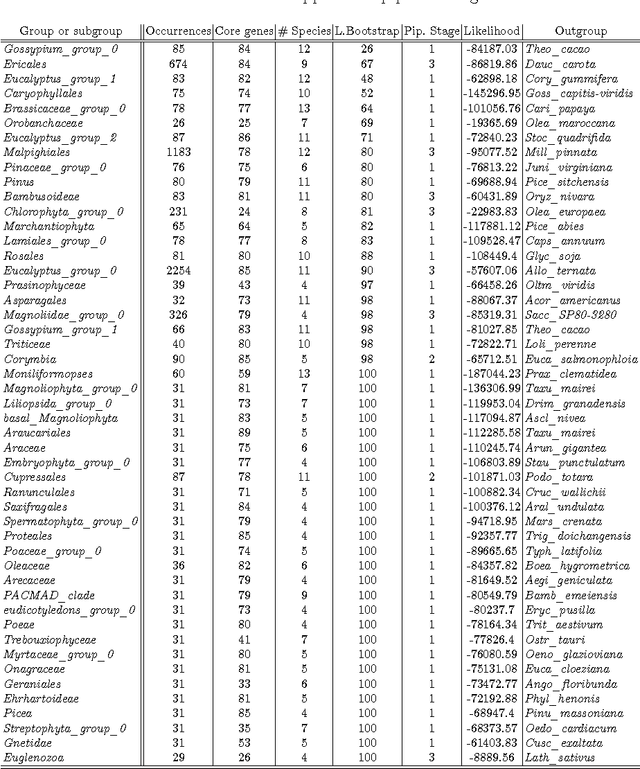
The amount of completely sequenced chloroplast genomes increases rapidly every day, leading to the possibility to build large scale phylogenetic trees of plant species. Considering a subset of close plant species defined according to their chloroplasts, the phylogenetic tree that can be inferred by their core genes is not necessarily well supported, due to the possible occurrence of "problematic" genes (i.e., homoplasy, incomplete lineage sorting, horizontal gene transfers, etc.) which may blur phylogenetic signal. However, a trustworthy phylogenetic tree can still be obtained if the number of problematic genes is low, the problem being to determine the largest subset of core genes that produces the best supported tree. To discard problematic genes and due to the overwhelming number of possible combinations, we propose an hybrid approach that embeds both genetic algorithms and statistical tests. Given a set of organisms, the result is a pipeline of many stages for the production of well supported phylogenetic trees. The proposal has been applied to different cases of plant families, leading to encouraging results for these families.

Gene Similarity-based Approaches for Determining Core-Genes of Chloroplasts

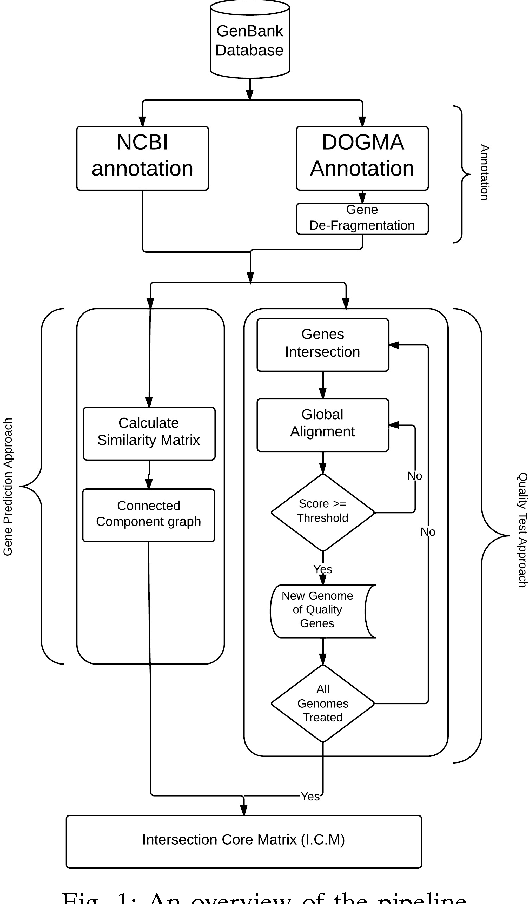
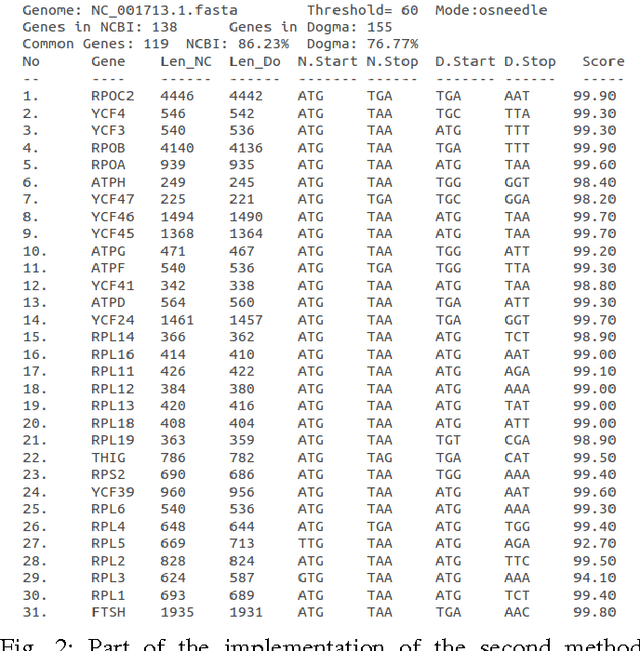
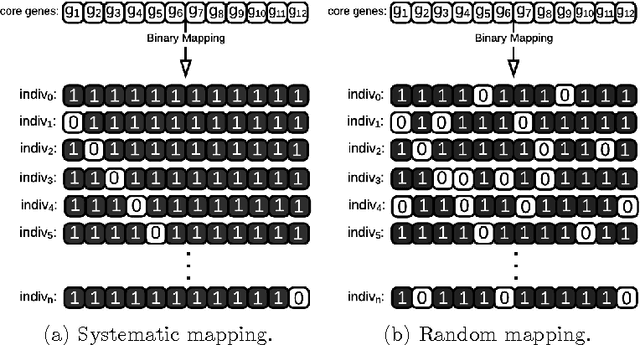
In computational biology and bioinformatics, the manner to understand evolution processes within various related organisms paid a lot of attention these last decades. However, accurate methodologies are still needed to discover genes content evolution. In a previous work, two novel approaches based on sequence similarities and genes features have been proposed. More precisely, we proposed to use genes names, sequence similarities, or both, insured either from NCBI or from DOGMA annotation tools. Dogma has the advantage to be an up-to-date accurate automatic tool specifically designed for chloroplasts, whereas NCBI possesses high quality human curated genes (together with wrongly annotated ones). The key idea of the former proposal was to take the best from these two tools. However, the first proposal was limited by name variations and spelling errors on the NCBI side, leading to core trees of low quality. In this paper, these flaws are fixed by improving the comparison of NCBI and DOGMA results, and by relaxing constraints on gene names while adding a stage of post-validation on gene sequences. The two stages of similarity measures, on names and sequences, are thus proposed for sequence clustering. This improves results that can be obtained using either NCBI or DOGMA alone. Results obtained with this quality control test are further investigated and compared with previously released ones, on both computational and biological aspects, considering a set of 99 chloroplastic genomes.

Building a Chaotic Proved Neural Network

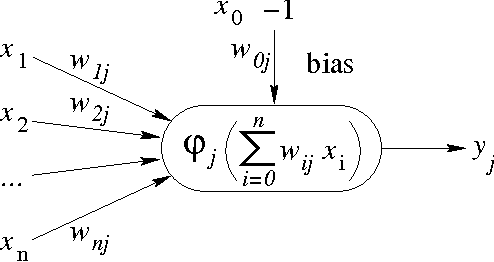
Chaotic neural networks have received a great deal of attention these last years. In this paper we establish a precise correspondence between the so-called chaotic iterations and a particular class of artificial neural networks: global recurrent multi-layer perceptrons. We show formally that it is possible to make these iterations behave chaotically, as defined by Devaney, and thus we obtain the first neural networks proven chaotic. Several neural networks with different architectures are trained to exhibit a chaotical behavior.