Zephyr quantum-assisted hierarchical Calo4pQVAE for particle-calorimeter interactions

With the approach of the High Luminosity Large Hadron Collider (HL-LHC) era set to begin particle collisions by the end of this decade, it is evident that the computational demands of traditional collision simulation methods are becoming increasingly unsustainable. Existing approaches, which rely heavily on first-principles Monte Carlo simulations for modeling event showers in calorimeters, are projected to require millions of CPU-years annually -- far exceeding current computational capacities. This bottleneck presents an exciting opportunity for advancements in computational physics by integrating deep generative models with quantum simulations. We propose a quantum-assisted hierarchical deep generative surrogate founded on a variational autoencoder (VAE) in combination with an energy conditioned restricted Boltzmann machine (RBM) embedded in the model's latent space as a prior. By mapping the topology of D-Wave's Zephyr quantum annealer (QA) into the nodes and couplings of a 4-partite RBM, we leverage quantum simulation to accelerate our shower generation times significantly. To evaluate our framework, we use Dataset 2 of the CaloChallenge 2022. Through the integration of classical computation and quantum simulation, this hybrid framework paves way for utilizing large-scale quantum simulations as priors in deep generative models.

Conditioned quantum-assisted deep generative surrogate for particle-calorimeter interactions

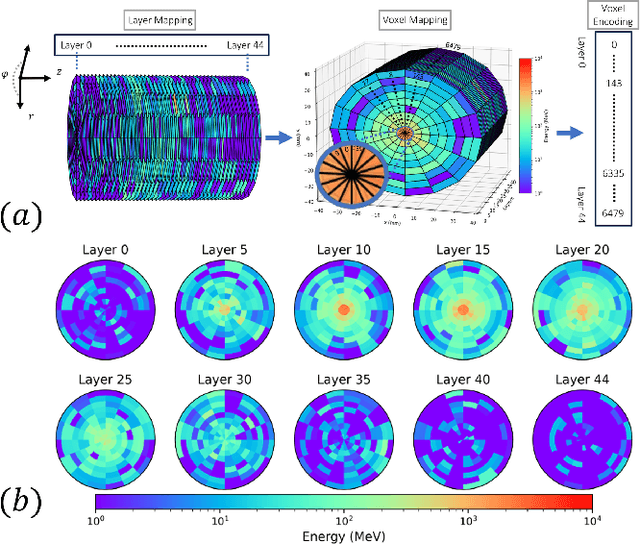
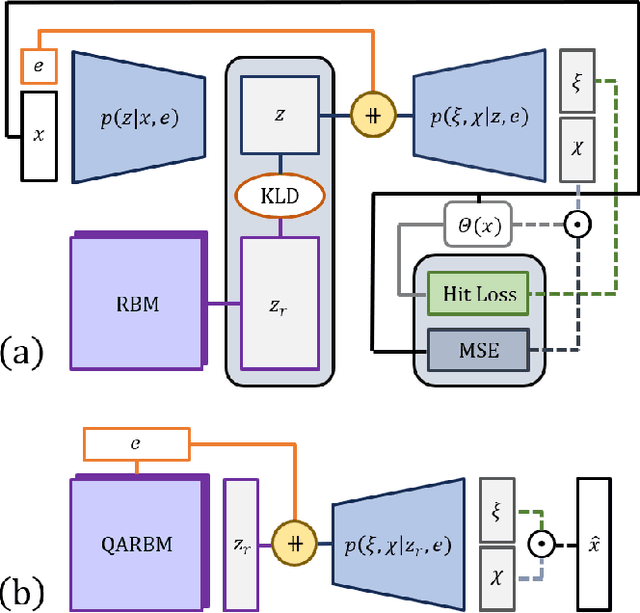
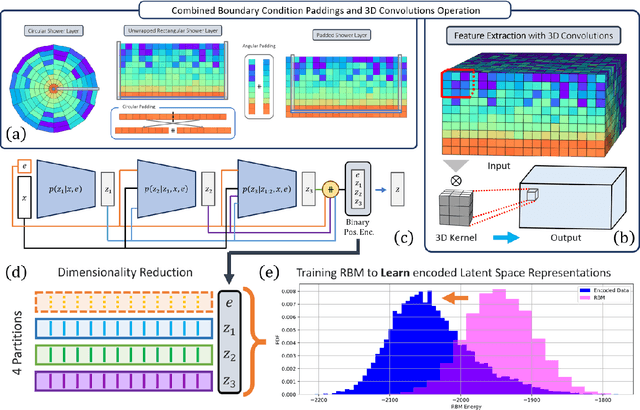
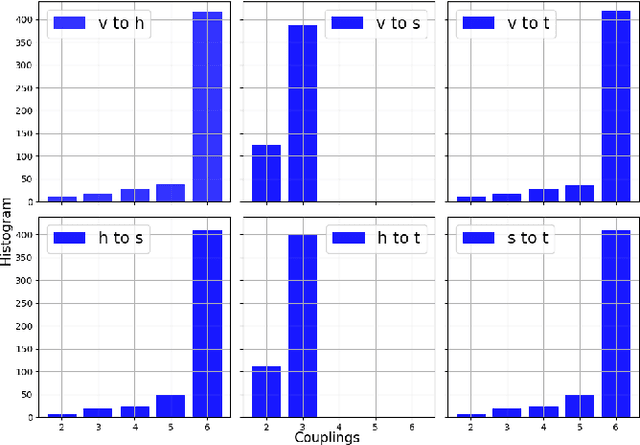
Particle collisions at accelerators such as the Large Hadron Collider, recorded and analyzed by experiments such as ATLAS and CMS, enable exquisite measurements of the Standard Model and searches for new phenomena. Simulations of collision events at these detectors have played a pivotal role in shaping the design of future experiments and analyzing ongoing ones. However, the quest for accuracy in Large Hadron Collider (LHC) collisions comes at an imposing computational cost, with projections estimating the need for millions of CPU-years annually during the High Luminosity LHC (HL-LHC) run \cite{collaboration2022atlas}. Simulating a single LHC event with \textsc{Geant4} currently devours around 1000 CPU seconds, with simulations of the calorimeter subdetectors in particular imposing substantial computational demands \cite{rousseau2023experimental}. To address this challenge, we propose a conditioned quantum-assisted deep generative model. Our model integrates a conditioned variational autoencoder (VAE) on the exterior with a conditioned Restricted Boltzmann Machine (RBM) in the latent space, providing enhanced expressiveness compared to conventional VAEs. The RBM nodes and connections are meticulously engineered to enable the use of qubits and couplers on D-Wave's Pegasus-structured \textit{Advantage} quantum annealer (QA) for sampling. We introduce a novel method for conditioning the quantum-assisted RBM using \textit{flux biases}. We further propose a novel adaptive mapping to estimate the effective inverse temperature in quantum annealers. The effectiveness of our framework is illustrated using Dataset 2 of the CaloChallenge \cite{calochallenge}.

Analyzing the Performance of Deep Encoder-Decoder Networks as Surrogates for a Diffusion Equation

Neural networks (NNs) have proven to be a viable alternative to traditional direct numerical algorithms, with the potential to accelerate computational time by several orders of magnitude. In the present paper we study the use of encoder-decoder convolutional neural network (CNN) as surrogates for steady-state diffusion solvers. The construction of such surrogates requires the selection of an appropriate task, network architecture, training set structure and size, loss function, and training algorithm hyperparameters. It is well known that each of these factors can have a significant impact on the performance of the resultant model. Our approach employs an encoder-decoder CNN architecture, which we posit is particularly well-suited for this task due to its ability to effectively transform data, as opposed to merely compressing it. We systematically evaluate a range of loss functions, hyperparameters, and training set sizes. Our results indicate that increasing the size of the training set has a substantial effect on reducing performance fluctuations and overall error. Additionally, we observe that the performance of the model exhibits a logarithmic dependence on the training set size. Furthermore, we investigate the effect on model performance by using different subsets of data with varying features. Our results highlight the importance of sampling the configurational space in an optimal manner, as this can have a significant impact on the performance of the model and the required training time. In conclusion, our results suggest that training a model with a pre-determined error performance bound is not a viable approach, as it does not guarantee that edge cases with errors larger than the bound do not exist. Furthermore, as most surrogate tasks involve a high dimensional landscape, an ever increasing training set size is, in principle, needed, however it is not a practical solution.

Using Deep LSD to build operators in GANs latent space with meaning in real space

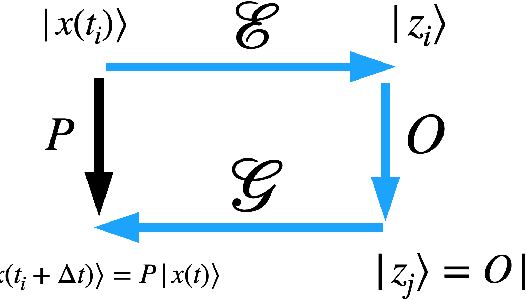
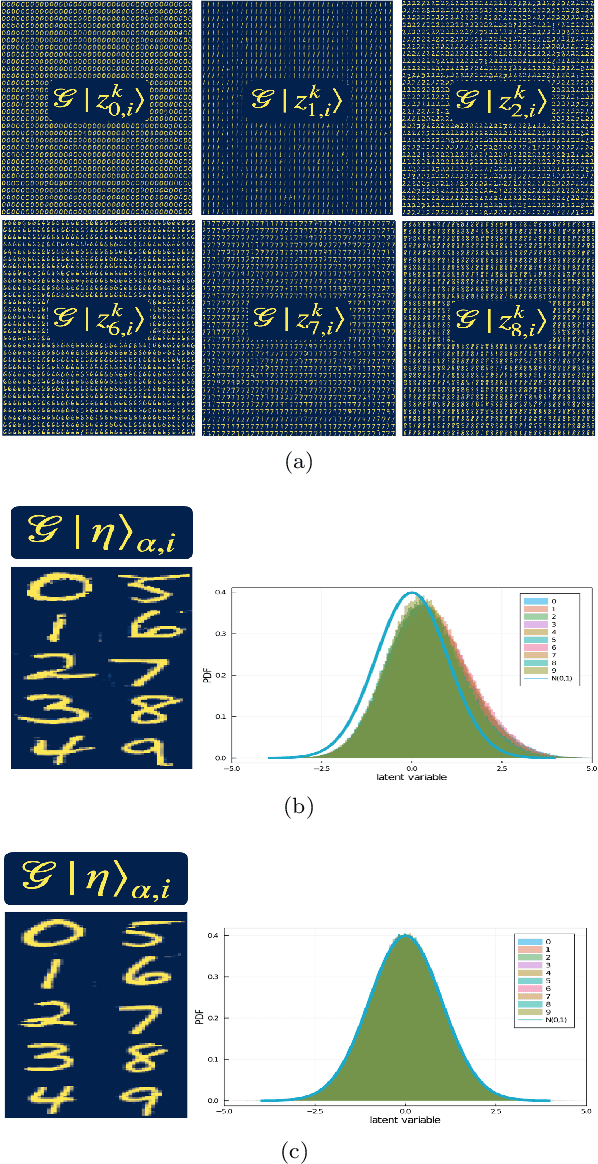
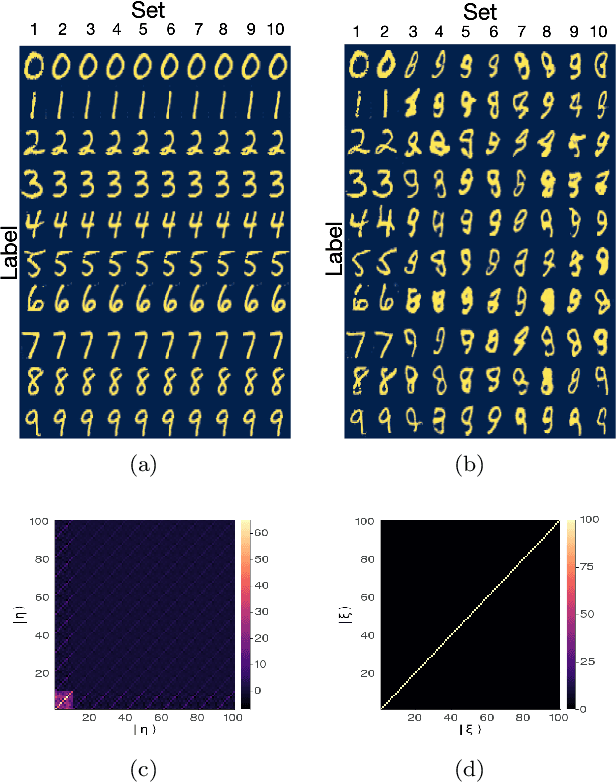
Generative models rely on the key idea that data can be represented in terms of latent variables which are uncorrelated by definition. Lack of correlation is important because it suggests that the latent space manifold is simpler to understand and manipulate. Generative models are widely used in deep learning, e.g., variational autoencoders (VAEs) and generative adversarial networks (GANs). Here we propose a method to build a set of linearly independent vectors in the latent space of a GANs, which we call quasi-eigenvectors. These quasi-eigenvectors have two key properties: i) They span all the latent space, ii) A set of these quasi-eigenvectors map to each of the labeled features one-on-one. We show that in the case of the MNIST, while the number of dimensions in latent space is large by construction, 98% of the data in real space map to a sub-domain of latent space of dimensionality equal to the number of labels. We then show how the quasi-eigenvalues can be used for Latent Spectral Decomposition (LSD), which has applications in denoising images and for performing matrix operations in latent space that map to feature transformations in real space. We show how this method provides insight into the latent space topology. The key point is that the set of quasi-eigenvectors form a basis set in latent space and each direction corresponds to a feature in real space.