Using Deep LSD to build operators in GANs latent space with meaning in real space
Paper and Code
Feb 09, 2021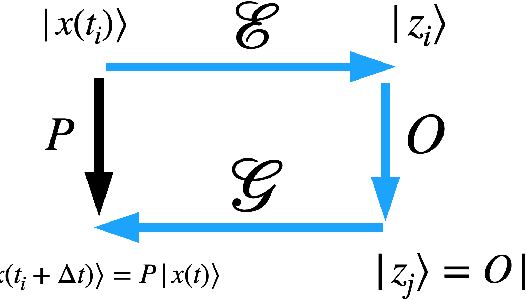

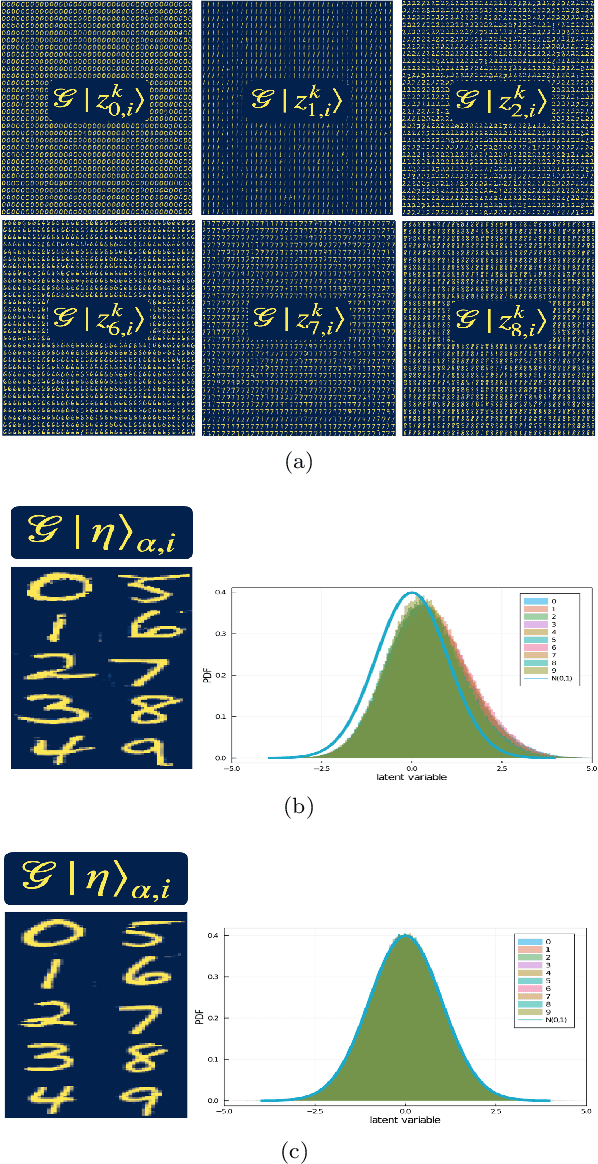
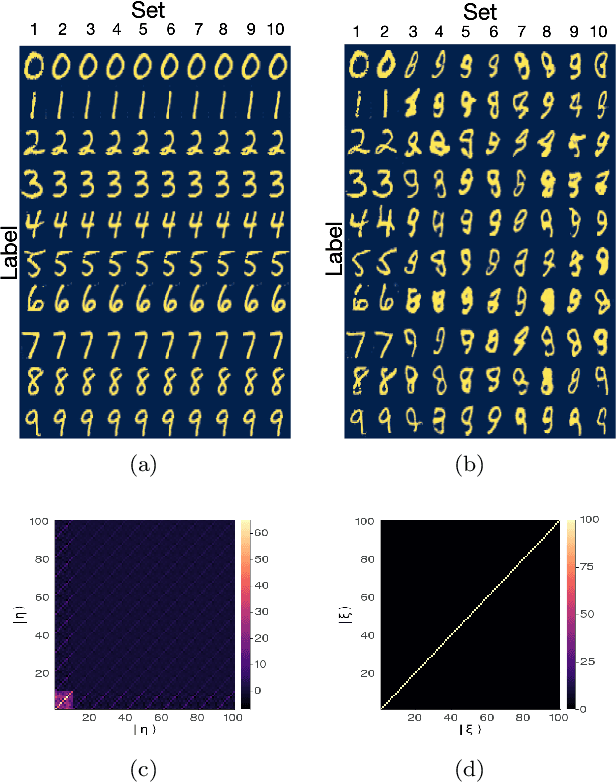
Generative models rely on the key idea that data can be represented in terms of latent variables which are uncorrelated by definition. Lack of correlation is important because it suggests that the latent space manifold is simpler to understand and manipulate. Generative models are widely used in deep learning, e.g., variational autoencoders (VAEs) and generative adversarial networks (GANs). Here we propose a method to build a set of linearly independent vectors in the latent space of a GANs, which we call quasi-eigenvectors. These quasi-eigenvectors have two key properties: i) They span all the latent space, ii) A set of these quasi-eigenvectors map to each of the labeled features one-on-one. We show that in the case of the MNIST, while the number of dimensions in latent space is large by construction, 98% of the data in real space map to a sub-domain of latent space of dimensionality equal to the number of labels. We then show how the quasi-eigenvalues can be used for Latent Spectral Decomposition (LSD), which has applications in denoising images and for performing matrix operations in latent space that map to feature transformations in real space. We show how this method provides insight into the latent space topology. The key point is that the set of quasi-eigenvectors form a basis set in latent space and each direction corresponds to a feature in real space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge