Analyzing the Performance of Deep Encoder-Decoder Networks as Surrogates for a Diffusion Equation

Neural networks (NNs) have proven to be a viable alternative to traditional direct numerical algorithms, with the potential to accelerate computational time by several orders of magnitude. In the present paper we study the use of encoder-decoder convolutional neural network (CNN) as surrogates for steady-state diffusion solvers. The construction of such surrogates requires the selection of an appropriate task, network architecture, training set structure and size, loss function, and training algorithm hyperparameters. It is well known that each of these factors can have a significant impact on the performance of the resultant model. Our approach employs an encoder-decoder CNN architecture, which we posit is particularly well-suited for this task due to its ability to effectively transform data, as opposed to merely compressing it. We systematically evaluate a range of loss functions, hyperparameters, and training set sizes. Our results indicate that increasing the size of the training set has a substantial effect on reducing performance fluctuations and overall error. Additionally, we observe that the performance of the model exhibits a logarithmic dependence on the training set size. Furthermore, we investigate the effect on model performance by using different subsets of data with varying features. Our results highlight the importance of sampling the configurational space in an optimal manner, as this can have a significant impact on the performance of the model and the required training time. In conclusion, our results suggest that training a model with a pre-determined error performance bound is not a viable approach, as it does not guarantee that edge cases with errors larger than the bound do not exist. Furthermore, as most surrogate tasks involve a high dimensional landscape, an ever increasing training set size is, in principle, needed, however it is not a practical solution.

Deep learning approaches to surrogates for solving the diffusion equation for mechanistic real-world simulations

In many mechanistic medical, biological, physical and engineered spatiotemporal dynamic models the numerical solution of partial differential equations (PDEs) can make simulations impractically slow. Biological models require the simultaneous calculation of the spatial variation of concentration of dozens of diffusing chemical species. Machine learning surrogates, neural networks trained to provide approximate solutions to such complicated numerical problems, can often provide speed-ups of several orders of magnitude compared to direct calculation. PDE surrogates enable use of larger models than are possible with direct calculation and can make including such simulations in real-time or near-real time workflows practical. Creating a surrogate requires running the direct calculation tens of thousands of times to generate training data and then training the neural network, both of which are computationally expensive. We use a Convolutional Neural Network to approximate the stationary solution to the diffusion equation in the case of two equal-diameter, circular, constant-value sources located at random positions in a two-dimensional square domain with absorbing boundary conditions. To improve convergence during training, we apply a training approach that uses roll-back to reject stochastic changes to the network that increase the loss function. The trained neural network approximation is about 1e3 times faster than the direct calculation for individual replicas. Because different applications will have different criteria for acceptable approximation accuracy, we discuss a variety of loss functions and accuracy estimators that can help select the best network for a particular application.

Using Deep LSD to build operators in GANs latent space with meaning in real space

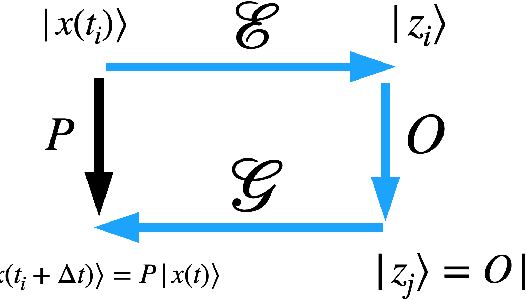
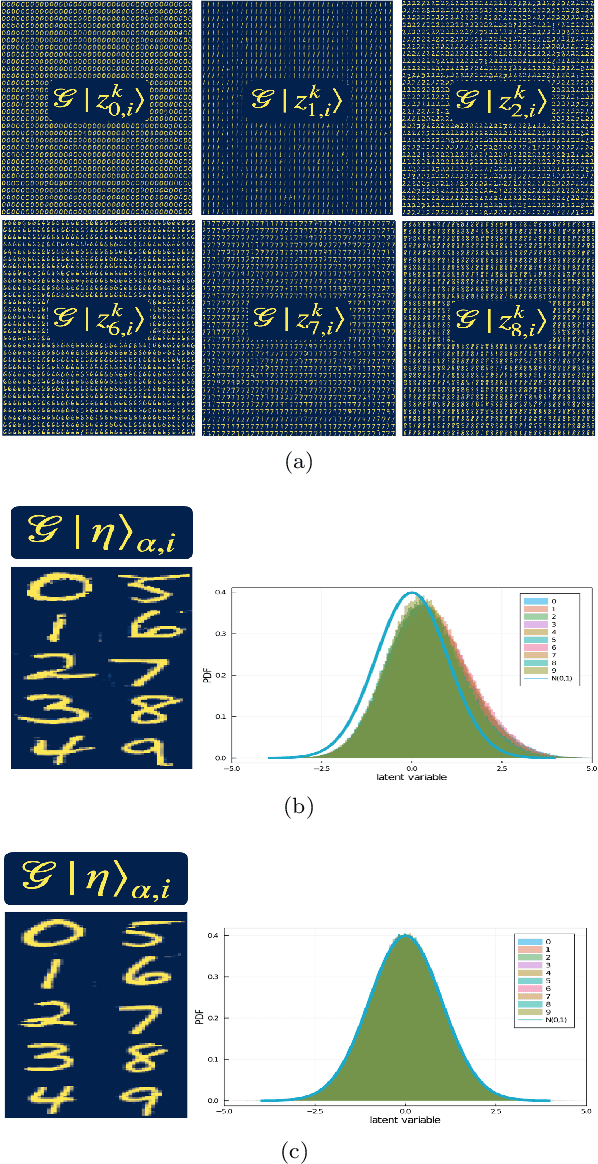
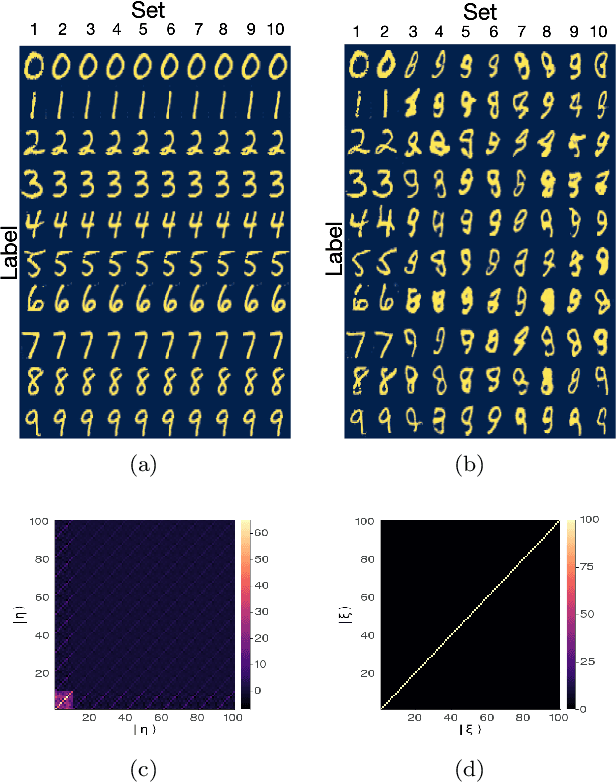
Generative models rely on the key idea that data can be represented in terms of latent variables which are uncorrelated by definition. Lack of correlation is important because it suggests that the latent space manifold is simpler to understand and manipulate. Generative models are widely used in deep learning, e.g., variational autoencoders (VAEs) and generative adversarial networks (GANs). Here we propose a method to build a set of linearly independent vectors in the latent space of a GANs, which we call quasi-eigenvectors. These quasi-eigenvectors have two key properties: i) They span all the latent space, ii) A set of these quasi-eigenvectors map to each of the labeled features one-on-one. We show that in the case of the MNIST, while the number of dimensions in latent space is large by construction, 98% of the data in real space map to a sub-domain of latent space of dimensionality equal to the number of labels. We then show how the quasi-eigenvalues can be used for Latent Spectral Decomposition (LSD), which has applications in denoising images and for performing matrix operations in latent space that map to feature transformations in real space. We show how this method provides insight into the latent space topology. The key point is that the set of quasi-eigenvectors form a basis set in latent space and each direction corresponds to a feature in real space.