Conditioned quantum-assisted deep generative surrogate for particle-calorimeter interactions

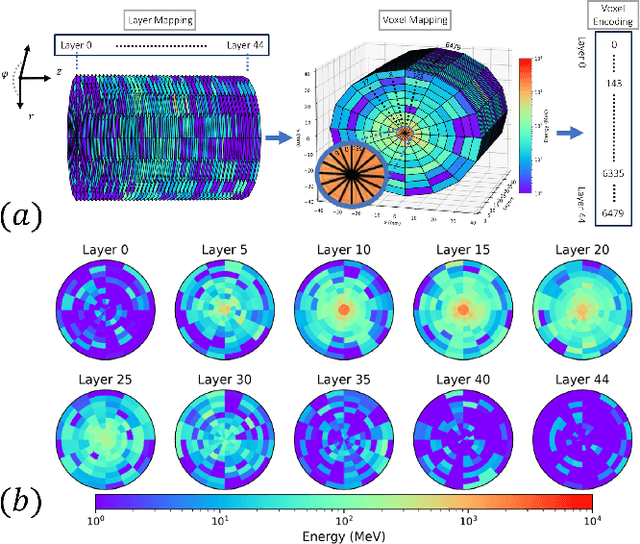
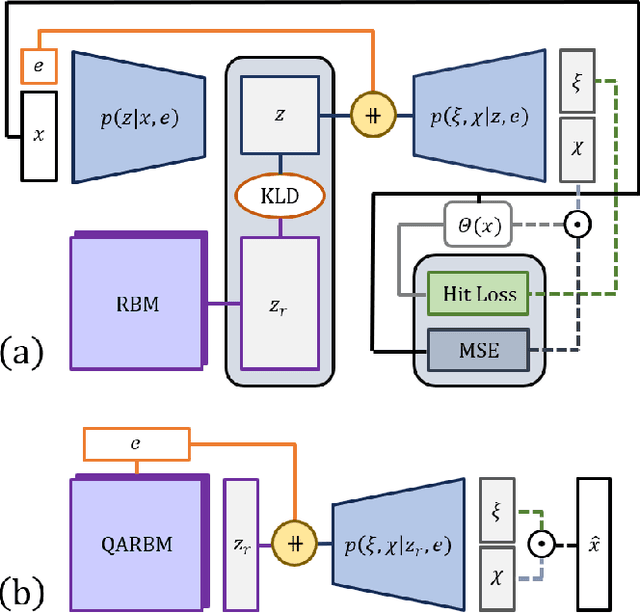
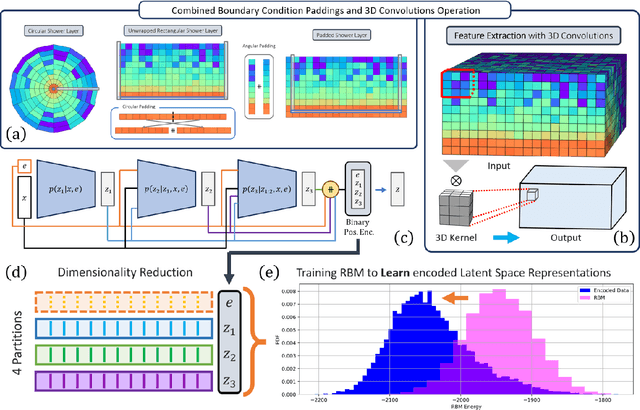
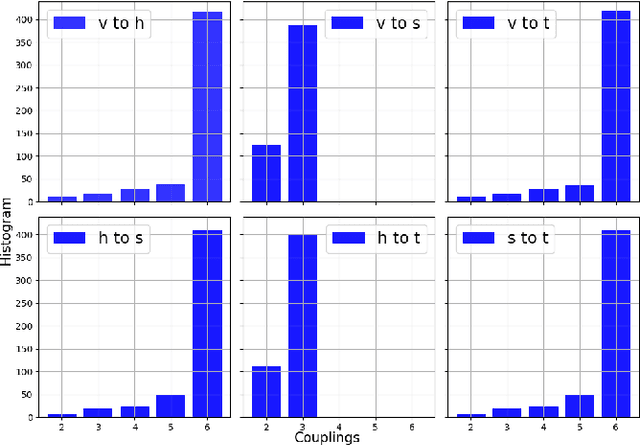
Particle collisions at accelerators such as the Large Hadron Collider, recorded and analyzed by experiments such as ATLAS and CMS, enable exquisite measurements of the Standard Model and searches for new phenomena. Simulations of collision events at these detectors have played a pivotal role in shaping the design of future experiments and analyzing ongoing ones. However, the quest for accuracy in Large Hadron Collider (LHC) collisions comes at an imposing computational cost, with projections estimating the need for millions of CPU-years annually during the High Luminosity LHC (HL-LHC) run \cite{collaboration2022atlas}. Simulating a single LHC event with \textsc{Geant4} currently devours around 1000 CPU seconds, with simulations of the calorimeter subdetectors in particular imposing substantial computational demands \cite{rousseau2023experimental}. To address this challenge, we propose a conditioned quantum-assisted deep generative model. Our model integrates a conditioned variational autoencoder (VAE) on the exterior with a conditioned Restricted Boltzmann Machine (RBM) in the latent space, providing enhanced expressiveness compared to conventional VAEs. The RBM nodes and connections are meticulously engineered to enable the use of qubits and couplers on D-Wave's Pegasus-structured \textit{Advantage} quantum annealer (QA) for sampling. We introduce a novel method for conditioning the quantum-assisted RBM using \textit{flux biases}. We further propose a novel adaptive mapping to estimate the effective inverse temperature in quantum annealers. The effectiveness of our framework is illustrated using Dataset 2 of the CaloChallenge \cite{calochallenge}.

The Accuracy of Restricted Boltzmann Machine Models of Ising Systems

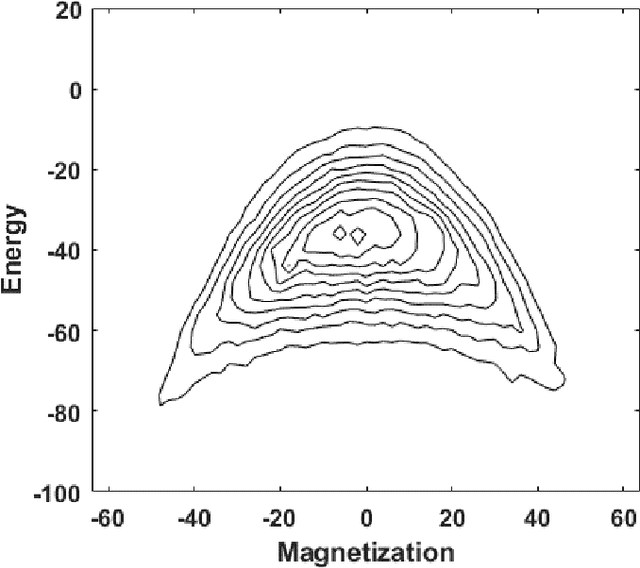
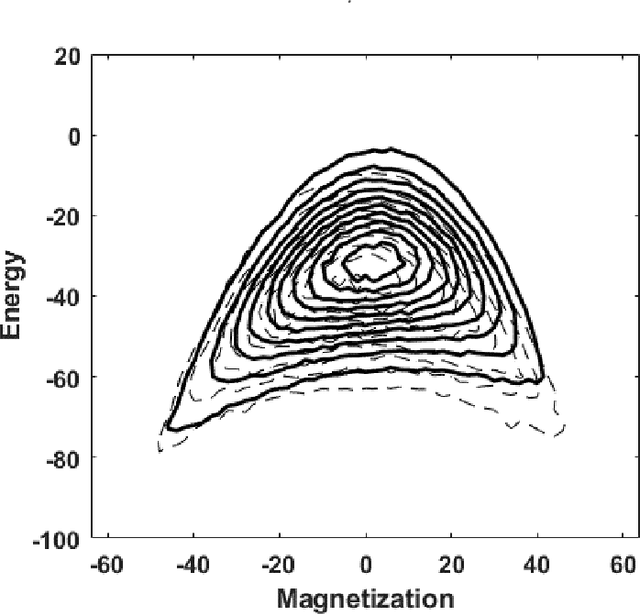
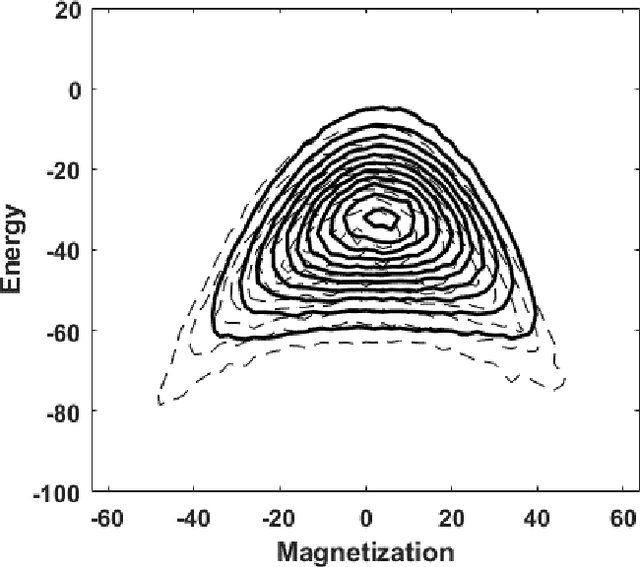
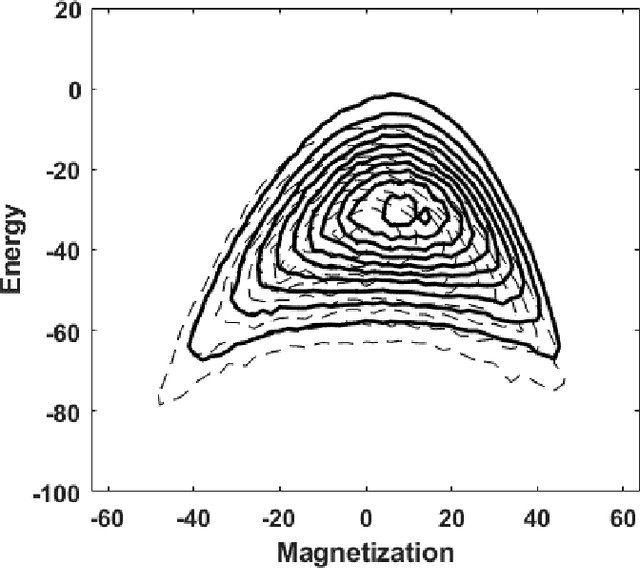
Restricted Boltzmann machine (RBM) provide a general framework for modeling physical systems, but their behavior is dependent on hyperparameters such as the learning rate, the number of hidden nodes and the form of the threshold function. This article accordingly examines in detail the influence of these parameters on Ising spin system calculations. A tradeoff is identified between the accuracy of statistical quantities such as the specific heat and that of the joint distribution of energy and magnetization. The optimal structure of the RBM therefore depends intrinsically on the physical problem to which it is applied.