Controlling Grokking with Nonlinearity and Data Symmetry

This paper demonstrates that grokking behavior in modular arithmetic with a modulus P in a neural network can be controlled by modifying the profile of the activation function as well as the depth and width of the model. Plotting the even PCA projections of the weights of the last NN layer against their odd projections further yields patterns which become significantly more uniform when the nonlinearity is increased by incrementing the number of layers. These patterns can be employed to factor P when P is nonprime. Finally, a metric for the generalization ability of the network is inferred from the entropy of the layer weights while the degree of nonlinearity is related to correlations between the local entropy of the weights of the neurons in the final layer.

Nonlinearity Enhanced Adaptive Activation Function

A simply implemented activation function with even cubic nonlinearity is introduced that increases the accuracy of neural networks without substantial additional computational resources. This is partially enabled through an apparent tradeoff between convergence and accuracy. The activation function generalizes the standard RELU function by introducing additional degrees of freedom through optimizable parameters that enable the degree of nonlinearity to be adjusted. The associated accuracy enhancement is quantified in the context of the MNIST digit data set through a comparison with standard techniques.

Branched Variational Autoencoder Classifiers

This paper introduces a modified variational autoencoder (VAEs) that contains an additional neural network branch. The resulting branched VAE (BVAE) contributes a classification component based on the class labels to the total loss and therefore imparts categorical information to the latent representation. As a result, the latent space distributions of the input classes are separated and ordered, thereby enhancing the classification accuracy. The degree of improvement is quantified by numerical calculations employing the benchmark MNIST dataset for both unrotated and rotated digits. The proposed technique is then compared to and then incorporated into a VAE with fixed output distributions. This procedure is found to yield improved performance for a wide range of output distributions.

Neural Network Characterization and Entropy Regulated Data Balancing through Principal Component Analysis

This paper examines the relationship between the behavior of a neural network and the distribution formed from the projections of the data records into the space spanned by the low-order principal components of the training data. For example, in a benchmark calculation involving rotated and unrotated MNIST digits, classes (digits) that are mapped far from the origin in a low-dimensional principal component space and that overlap minimally with other digits converge rapidly and exhibit high degrees of accuracy in neural network calculations that employ the associated components of each data record as inputs. Further, if the space spanned by these low-order principal components is divided into bins and the input data records that are mapped into a given bin averaged, the resulting pattern can be distinguished by its geometric features which interpolate between those of adjacent bins in an analogous manner to variational autoencoders. Based on this observation, a simply realized data balancing procedure can be realized by evaluating the entropy associated with each histogram bin and subsequently repeating the original image data associated with the bin by a number of times that is determined from this entropy.

Rotated Digit Recognition by Variational Autoencoders with Fixed Output Distributions

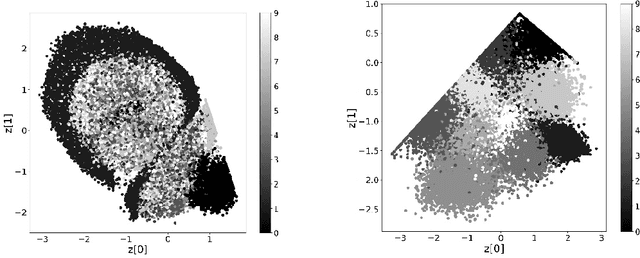
This paper demonstrates that a simple modification of the variational autoencoder (VAE) formalism enables the method to identify and classify rotated and distorted digits. In particular, the conventional objective (cost) function employed during the training process of a VAE both quantifies the agreement between the input and output data records and ensures that the latent space representation of the input data record is statistically generated with an appropriate mean and standard deviation. After training, simulated data realizations are generated by decoding appropriate latent space points. Since, however, standard VAE:s trained on randomly rotated MNIST digits cannot reliably distinguish between different digit classes since the rotated input data is effectively compared to a similarly rotated output data record. In contrast, an alternative implementation in which the objective function compares the output associated with each rotated digit to a corresponding fixed unreferenced reference digit is shown here to discriminate accurately among the rotated digits in latent space even when the dimension of the latent space is 2 or 3.

Variational Autoencoder Analysis of Ising Model Statistical Distributions and Phase Transitions

Variational autoencoders employ an encoding neural network to generate a probabilistic representation of a data set within a low-dimensional space of latent variables followed by a decoding stage that maps the latent variables back to the original variable space. Once trained, a statistical ensemble of simulated data realizations can be obtained by randomly assigning values to the latent variables that are subsequently processed by the decoding section of the network. To determine the accuracy of such a procedure when applied to lattice models, an autoencoder is here trained on a thermal equilibrium distribution of Ising spin realizations. When the output of the decoder for synthetic data is interpreted probabilistically, spin realizations can be generated by randomly assigning spin values according to the computed likelihood. The resulting state distribution in energy-magnetization space then qualitatively resembles that of the training samples. However, because correlations between spins are suppressed, the computed energies are unphysically large for low-dimensional latent variable spaces. The features of the learned distributions as a function of temperature, however, provide a qualitative indication of the presence of a phase transition and the distribution of realizations with characteristic cluster sizes.

The Accuracy of Restricted Boltzmann Machine Models of Ising Systems

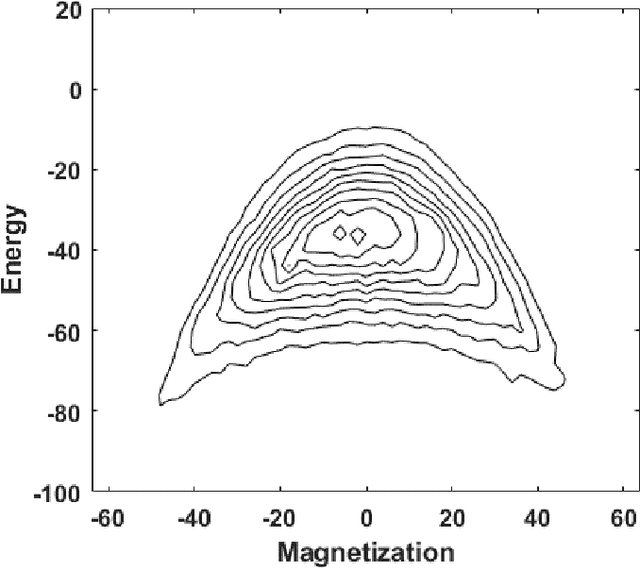
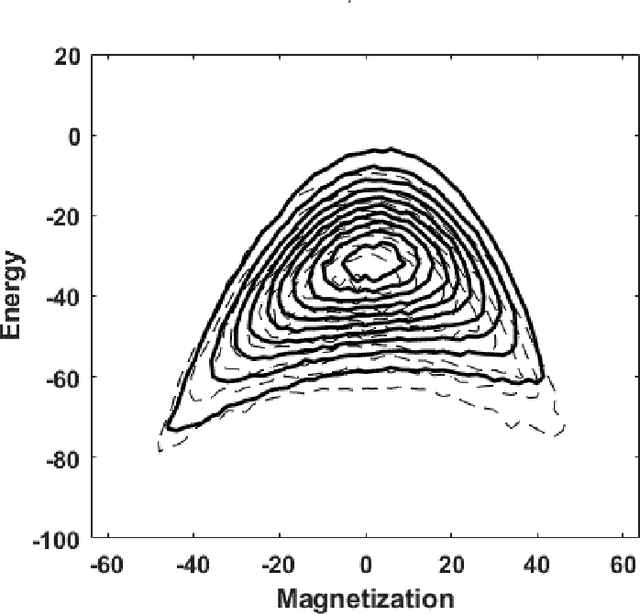
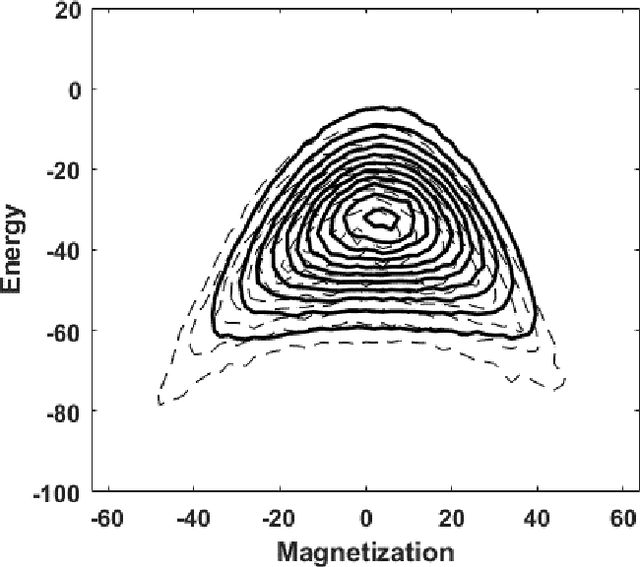
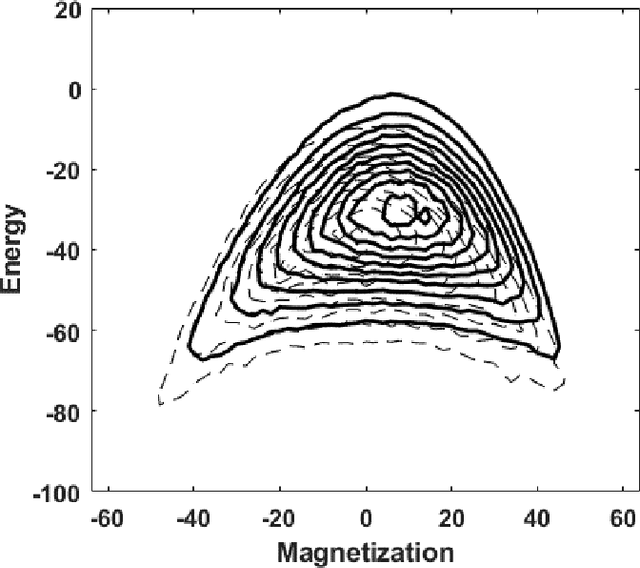
Restricted Boltzmann machine (RBM) provide a general framework for modeling physical systems, but their behavior is dependent on hyperparameters such as the learning rate, the number of hidden nodes and the form of the threshold function. This article accordingly examines in detail the influence of these parameters on Ising spin system calculations. A tradeoff is identified between the accuracy of statistical quantities such as the specific heat and that of the joint distribution of energy and magnetization. The optimal structure of the RBM therefore depends intrinsically on the physical problem to which it is applied.