Rotated Digit Recognition by Variational Autoencoders with Fixed Output Distributions
Paper and Code
Jun 18, 2022


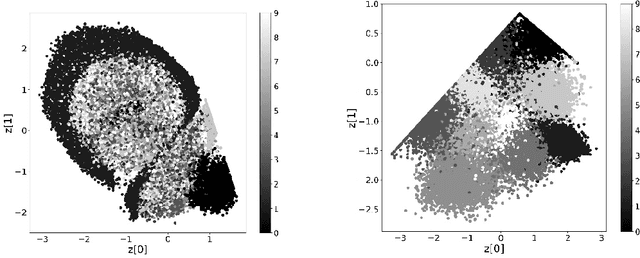
This paper demonstrates that a simple modification of the variational autoencoder (VAE) formalism enables the method to identify and classify rotated and distorted digits. In particular, the conventional objective (cost) function employed during the training process of a VAE both quantifies the agreement between the input and output data records and ensures that the latent space representation of the input data record is statistically generated with an appropriate mean and standard deviation. After training, simulated data realizations are generated by decoding appropriate latent space points. Since, however, standard VAE:s trained on randomly rotated MNIST digits cannot reliably distinguish between different digit classes since the rotated input data is effectively compared to a similarly rotated output data record. In contrast, an alternative implementation in which the objective function compares the output associated with each rotated digit to a corresponding fixed unreferenced reference digit is shown here to discriminate accurately among the rotated digits in latent space even when the dimension of the latent space is 2 or 3.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge