Learning Causally Invariant Reward Functions from Diverse Demonstrations

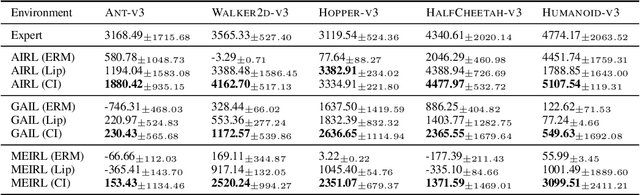
Inverse reinforcement learning methods aim to retrieve the reward function of a Markov decision process based on a dataset of expert demonstrations. The commonplace scarcity and heterogeneous sources of such demonstrations can lead to the absorption of spurious correlations in the data by the learned reward function. Consequently, this adaptation often exhibits behavioural overfitting to the expert data set when a policy is trained on the obtained reward function under distribution shift of the environment dynamics. In this work, we explore a novel regularization approach for inverse reinforcement learning methods based on the causal invariance principle with the goal of improved reward function generalization. By applying this regularization to both exact and approximate formulations of the learning task, we demonstrate superior policy performance when trained using the recovered reward functions in a transfer setting

Regularizing Adversarial Imitation Learning Using Causal Invariance

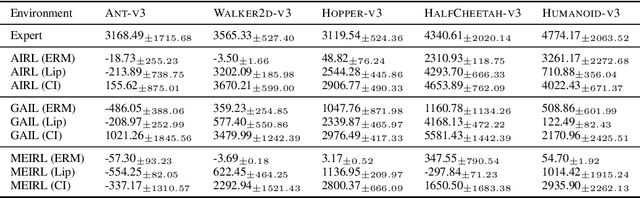
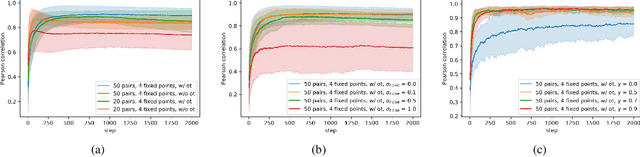
Imitation learning methods are used to infer a policy in a Markov decision process from a dataset of expert demonstrations by minimizing a divergence measure between the empirical state occupancy measures of the expert and the policy. The guiding signal to the policy is provided by the discriminator used as part of an versarial optimization procedure. We observe that this model is prone to absorbing spurious correlations present in the expert data. To alleviate this issue, we propose to use causal invariance as a regularization principle for adversarial training of these models. The regularization objective is applicable in a straightforward manner to existing adversarial imitation frameworks. We demonstrate the efficacy of the regularized formulation in an illustrative two-dimensional setting as well as a number of high-dimensional robot locomotion benchmark tasks.

Inverse Reinforcement Learning via Matching of Optimality Profiles

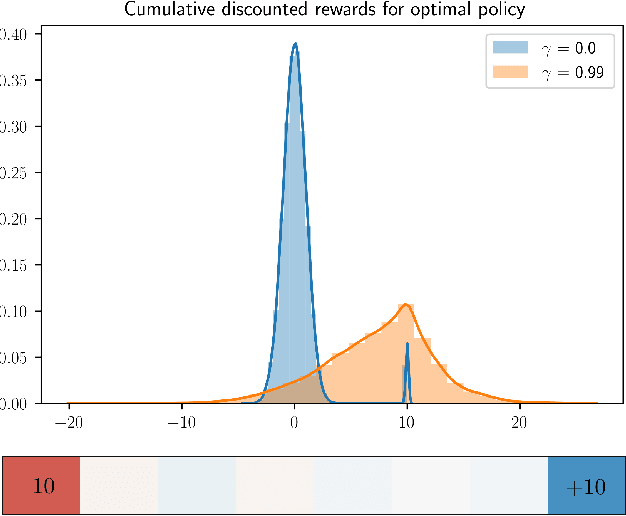
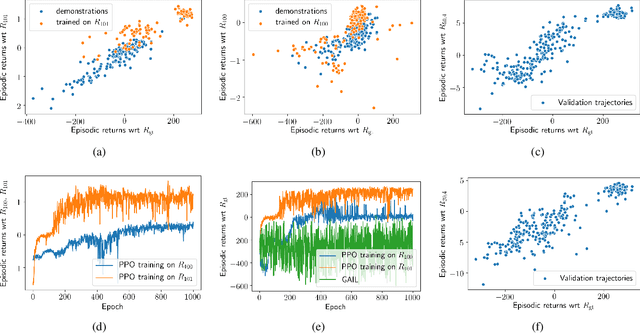
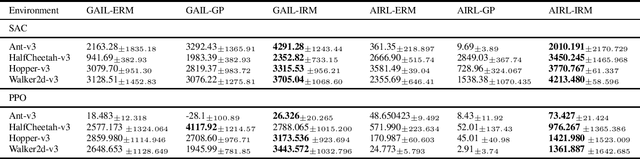
The goal of inverse reinforcement learning (IRL) is to infer a reward function that explains the behavior of an agent performing a task. The assumption that most approaches make is that the demonstrated behavior is near-optimal. In many real-world scenarios, however, examples of truly optimal behavior are scarce, and it is desirable to effectively leverage sets of demonstrations of suboptimal or heterogeneous performance, which are easier to obtain. We propose an algorithm that learns a reward function from such demonstrations together with a weak supervision signal in the form of a distribution over rewards collected during the demonstrations (or, more generally, a distribution over cumulative discounted future rewards). We view such distributions, which we also refer to as optimality profiles, as summaries of the degree of optimality of the demonstrations that may, for example, reflect the opinion of a human expert. Given an optimality profile and a small amount of additional supervision, our algorithm fits a reward function, modeled as a neural network, by essentially minimizing the Wasserstein distance between the corresponding induced distribution and the optimality profile. We show that our method is capable of learning reward functions such that policies trained to optimize them outperform the demonstrations used for fitting the reward functions.

Poincaré Wasserstein Autoencoder

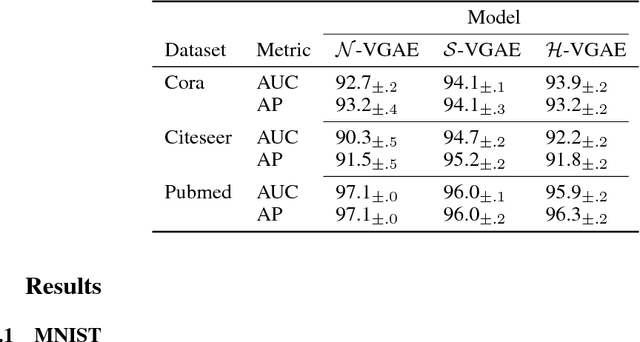
This work presents a reformulation of the recently proposed Wasserstein autoencoder framework on a non-Euclidean manifold, the Poincar\'e ball model of the hyperbolic space. By assuming the latent space to be hyperbolic, we can use its intrinsic hierarchy to impose structure on the learned latent space representations. We demonstrate the model in the visual domain to analyze some of its properties and show competitive results on a graph link prediction task.