Inverse Reinforcement Learning via Matching of Optimality Profiles
Paper and Code
Nov 19, 2020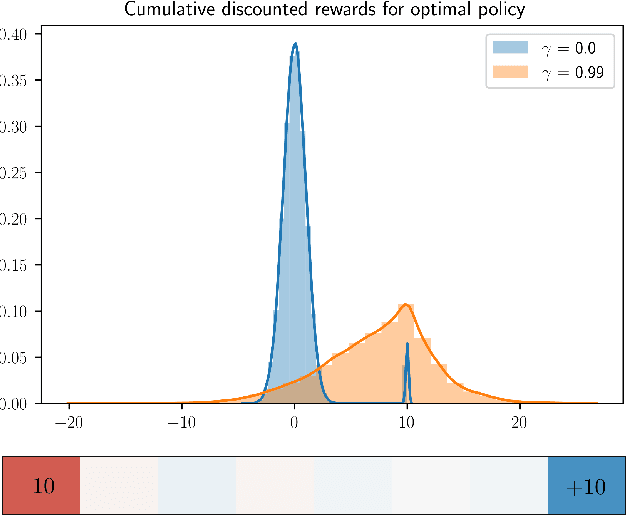

The goal of inverse reinforcement learning (IRL) is to infer a reward function that explains the behavior of an agent performing a task. The assumption that most approaches make is that the demonstrated behavior is near-optimal. In many real-world scenarios, however, examples of truly optimal behavior are scarce, and it is desirable to effectively leverage sets of demonstrations of suboptimal or heterogeneous performance, which are easier to obtain. We propose an algorithm that learns a reward function from such demonstrations together with a weak supervision signal in the form of a distribution over rewards collected during the demonstrations (or, more generally, a distribution over cumulative discounted future rewards). We view such distributions, which we also refer to as optimality profiles, as summaries of the degree of optimality of the demonstrations that may, for example, reflect the opinion of a human expert. Given an optimality profile and a small amount of additional supervision, our algorithm fits a reward function, modeled as a neural network, by essentially minimizing the Wasserstein distance between the corresponding induced distribution and the optimality profile. We show that our method is capable of learning reward functions such that policies trained to optimize them outperform the demonstrations used for fitting the reward functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge