Poincaré Wasserstein Autoencoder
Paper and Code
Jan 05, 2019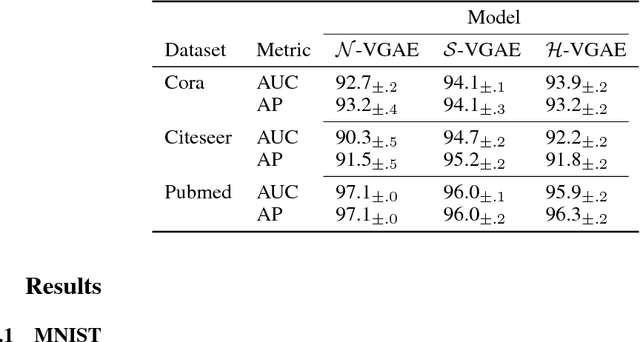


This work presents a reformulation of the recently proposed Wasserstein autoencoder framework on a non-Euclidean manifold, the Poincar\'e ball model of the hyperbolic space. By assuming the latent space to be hyperbolic, we can use its intrinsic hierarchy to impose structure on the learned latent space representations. We demonstrate the model in the visual domain to analyze some of its properties and show competitive results on a graph link prediction task.
* Bayesian Deep Learning Workshop (NeurIPS 2018)
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge