Ontology-driven Prompt Tuning for LLM-based Task and Motion Planning

Performing complex manipulation tasks in dynamic environments requires efficient Task and Motion Planning (TAMP) approaches, which combine high-level symbolic plan with low-level motion planning. Advances in Large Language Models (LLMs), such as GPT-4, are transforming task planning by offering natural language as an intuitive and flexible way to describe tasks, generate symbolic plans, and reason. However, the effectiveness of LLM-based TAMP approaches is limited due to static and template-based prompting, which struggles in adapting to dynamic environments and complex task contexts. To address these limitations, this work proposes a novel ontology-driven prompt-tuning framework that employs knowledge-based reasoning to refine and expand user prompts with task contextual reasoning and knowledge-based environment state descriptions. Integrating domain-specific knowledge into the prompt ensures semantically accurate and context-aware task plans. The proposed framework demonstrates its effectiveness by resolving semantic errors in symbolic plan generation, such as maintaining logical temporal goal ordering in scenarios involving hierarchical object placement. The proposed framework is validated through both simulation and real-world scenarios, demonstrating significant improvements over the baseline approach in terms of adaptability to dynamic environments, and the generation of semantically correct task plans.

Symbolic and User-friendly Geometric Algebra Routines (SUGAR) for Computations in Matlab

Geometric algebra (GA) is a mathematical tool for geometric computing, providing a framework that allows a unified and compact approach to geometric relations which in other mathematical systems are typically described using different more complicated elements. This fact has led to an increasing adoption of GA in applied mathematics and engineering problems. However, the scarcity of symbolic implementations of GA and its inherent complexity, requiring a specific mathematical background, make it challenging and less intuitive for engineers to work with. This prevents wider adoption among more applied professionals. To address this challenge, this paper introduces SUGAR (Symbolic and User-friendly Geometric Algebra Routines), an open-source toolbox designed for Matlab and licensed under the MIT License. SUGAR facilitates the translation of GA concepts into Matlab and provides a collection of user-friendly functions tailored for GA computations, including support for symbolic operations. It supports both numeric and symbolic computations in high-dimensional GAs. Specifically tailored for applied mathematics and engineering applications, SUGAR has been meticulously engineered to represent geometric elements and transformations within two and three-dimensional projective and conformal geometric algebras, aligning with established computational methodologies in the literature. Furthermore, SUGAR efficiently handles functions of multivectors, such as exponential, logarithmic, sinusoidal, and cosine functions, enhancing its applicability across various engineering domains, including robotics, control systems, and power electronics. Finally, this work includes four distinct validation examples, demonstrating SUGAR's capabilities across the above-mentioned fields and its practical utility in addressing real-world applied mathematics and engineering problems.

Singularities of serial robots: Identification and distance computation using geometric algebra

The singularities of serial robotic manipulators are those configurations in which the robot loses the ability to move in at least one direction. Hence, their identification is fundamental to enhance the performance of current control and motion planning strategies. While classical approaches entail the computation of the determinant of either a 6x n or nxn matrix for an n degrees of freedom serial robot, this work addresses a novel singularity identification method based on modelling the twists defined by the joint axes of the robot as vectors of the six-dimensional and three-dimensional geometric algebras. In particular, it consists of identifying which configurations cause the exterior product of these twists to vanish. In addition, since rotors represent rotations in geometric algebra, once these singularities have been identified, a distance function is defined in the configuration space C such that its restriction to the set of singular configurations S allows us to compute the distance of any configuration to a given singularity. This distance function is used to enhance how the singularities are handled in three different scenarios, namely motion planning, motion control and bilateral teleoperation.

Closed-form solutions for the inverse kinematics of serial robots using conformal geometric algebra

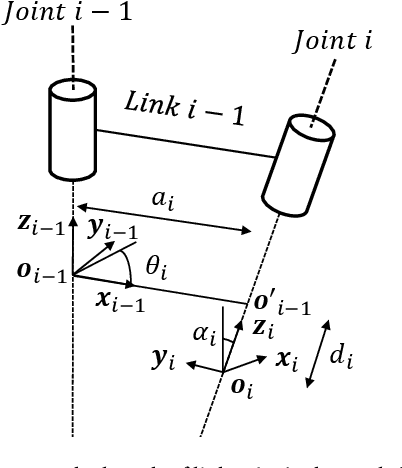
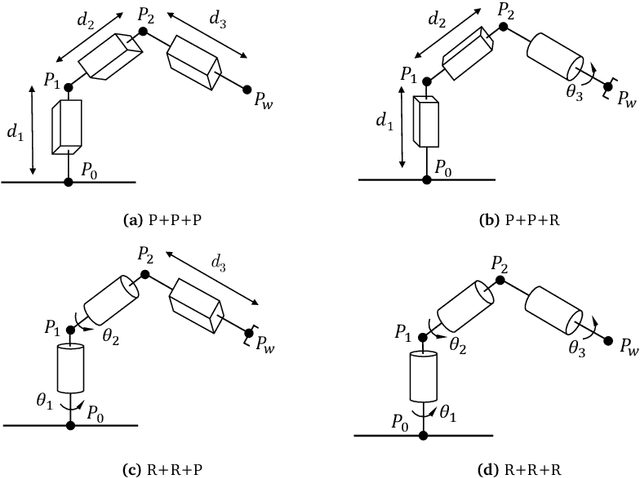
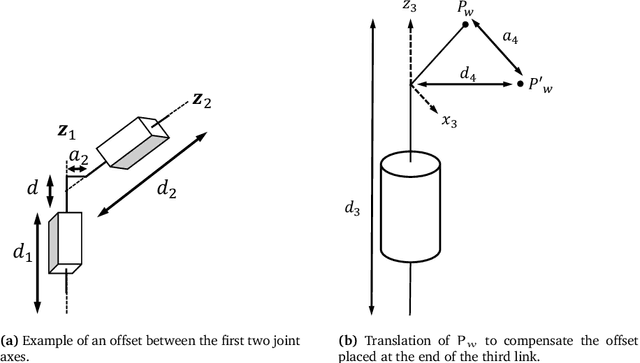
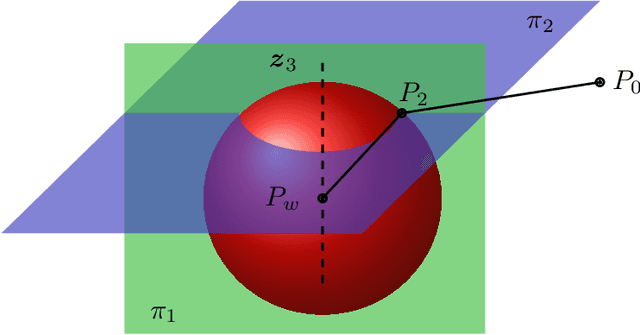
This work addresses the inverse kinematics of serial robots using conformal geometric algebra. Classical approaches include either the use of homogeneous matrices, which entails high computational cost and execution time or the development of particular geometric strategies that cannot be generalized to arbitrary serial robots. In this work, we present a compact, elegant and intuitive formulation of robot kinematics based on conformal geometric algebra that provides a suitable framework for the closed-form resolution of the inverse kinematic problem for manipulators with a spherical wrist. For serial robots of this kind, the inverse kinematics problem can be split in two subproblems: the position and orientation problems. The latter is solved by appropriately splitting the rotor that defines the target orientation into three simpler rotors, while the former is solved by developing a geometric strategy for each combination of prismatic and revolute joints that forms the position part of the robot. Finally, the inverse kinematics of 7 DoF redundant manipulators with a spherical wrist is solved by extending the geometric solutions obtained in the non-redundant case.