Singularities of serial robots: Identification and distance computation using geometric algebra

The singularities of serial robotic manipulators are those configurations in which the robot loses the ability to move in at least one direction. Hence, their identification is fundamental to enhance the performance of current control and motion planning strategies. While classical approaches entail the computation of the determinant of either a 6x n or nxn matrix for an n degrees of freedom serial robot, this work addresses a novel singularity identification method based on modelling the twists defined by the joint axes of the robot as vectors of the six-dimensional and three-dimensional geometric algebras. In particular, it consists of identifying which configurations cause the exterior product of these twists to vanish. In addition, since rotors represent rotations in geometric algebra, once these singularities have been identified, a distance function is defined in the configuration space C such that its restriction to the set of singular configurations S allows us to compute the distance of any configuration to a given singularity. This distance function is used to enhance how the singularities are handled in three different scenarios, namely motion planning, motion control and bilateral teleoperation.

Closed-form solutions for the inverse kinematics of serial robots using conformal geometric algebra

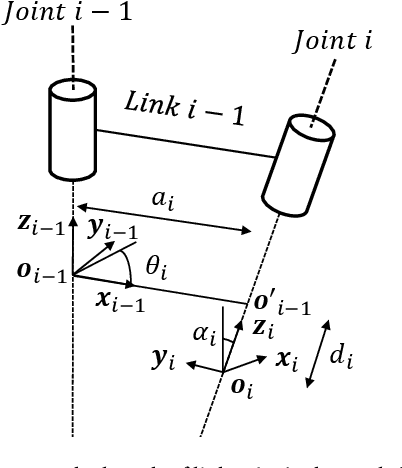
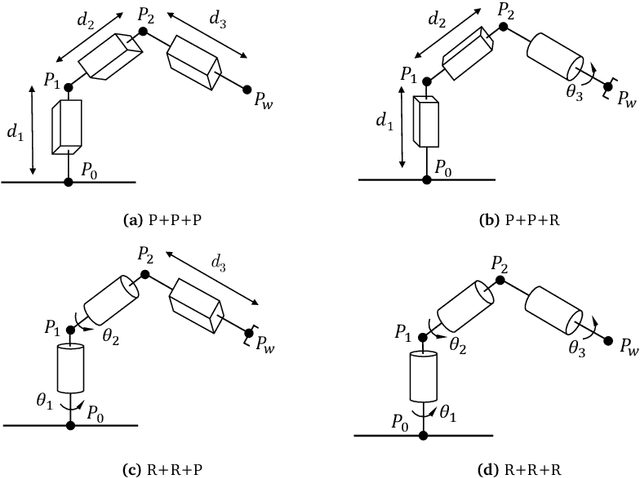
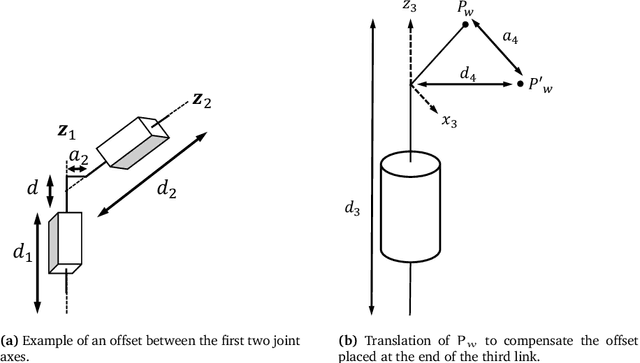
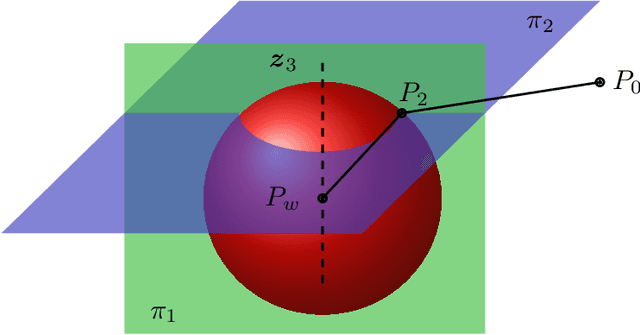
This work addresses the inverse kinematics of serial robots using conformal geometric algebra. Classical approaches include either the use of homogeneous matrices, which entails high computational cost and execution time or the development of particular geometric strategies that cannot be generalized to arbitrary serial robots. In this work, we present a compact, elegant and intuitive formulation of robot kinematics based on conformal geometric algebra that provides a suitable framework for the closed-form resolution of the inverse kinematic problem for manipulators with a spherical wrist. For serial robots of this kind, the inverse kinematics problem can be split in two subproblems: the position and orientation problems. The latter is solved by appropriately splitting the rotor that defines the target orientation into three simpler rotors, while the former is solved by developing a geometric strategy for each combination of prismatic and revolute joints that forms the position part of the robot. Finally, the inverse kinematics of 7 DoF redundant manipulators with a spherical wrist is solved by extending the geometric solutions obtained in the non-redundant case.