Closed-form solutions for the inverse kinematics of serial robots using conformal geometric algebra

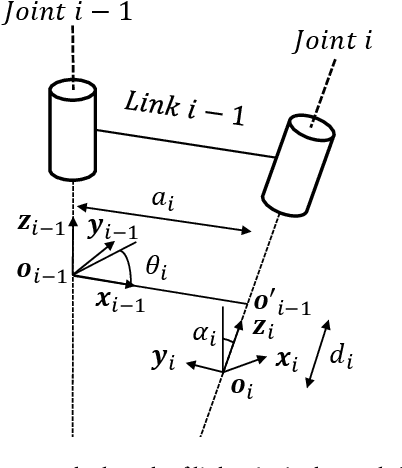
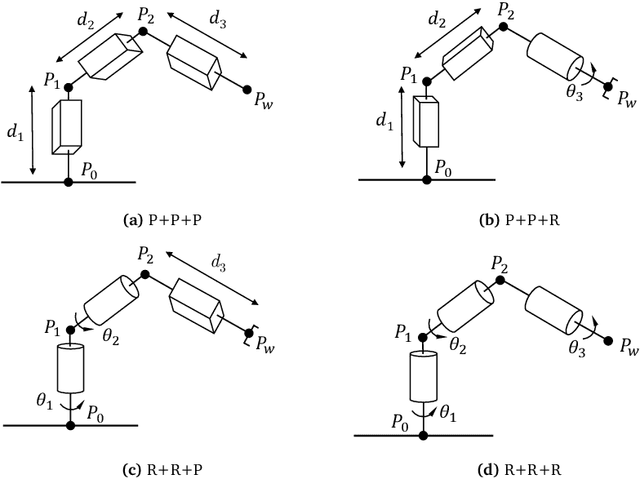
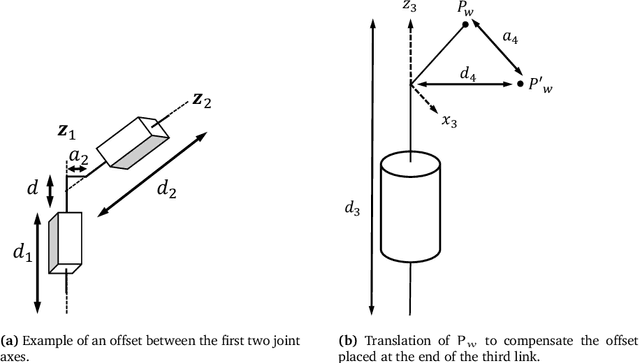
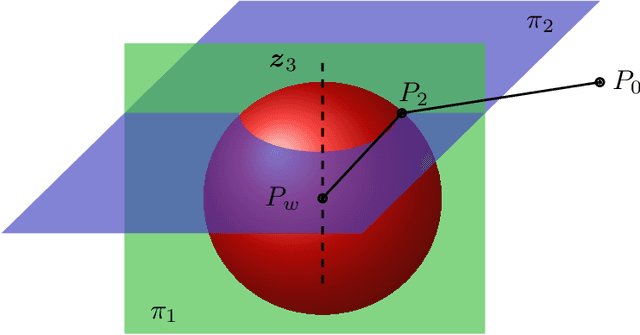
This work addresses the inverse kinematics of serial robots using conformal geometric algebra. Classical approaches include either the use of homogeneous matrices, which entails high computational cost and execution time or the development of particular geometric strategies that cannot be generalized to arbitrary serial robots. In this work, we present a compact, elegant and intuitive formulation of robot kinematics based on conformal geometric algebra that provides a suitable framework for the closed-form resolution of the inverse kinematic problem for manipulators with a spherical wrist. For serial robots of this kind, the inverse kinematics problem can be split in two subproblems: the position and orientation problems. The latter is solved by appropriately splitting the rotor that defines the target orientation into three simpler rotors, while the former is solved by developing a geometric strategy for each combination of prismatic and revolute joints that forms the position part of the robot. Finally, the inverse kinematics of 7 DoF redundant manipulators with a spherical wrist is solved by extending the geometric solutions obtained in the non-redundant case.