PDE-Based Optimal Strategy for Unconstrained Online Learning

Unconstrained Online Linear Optimization (OLO) is a practical problem setting to study the training of machine learning models. Existing works proposed a number of potential-based algorithms, but in general the design of such potential functions is ad hoc and heavily relies on guessing. In this paper, we present a framework that generates time-varying potential functions by solving a Partial Differential Equation (PDE). Our framework recovers some classical potentials, and more importantly provides a systematic approach to design new ones. The power of our framework is demonstrated through a concrete example. When losses are 1-Lipschitz, we design a novel OLO algorithm with anytime regret upper bound $C\sqrt{T}+||u||\sqrt{2T}[\sqrt{\log(1+||u||/C)}+2]$, where $C$ is a user-specified constant and $u$ is any comparator whose norm is unknown and unbounded a priori. By constructing a matching lower bound, we further show that the leading order term, including the constant multiplier $\sqrt{2}$, is tight. To our knowledge, this is the first parameter-free algorithm with optimal leading constant. The obtained theoretical benefits are validated by experiments.

Distributionally Robust Multi-Output Regression Ranking

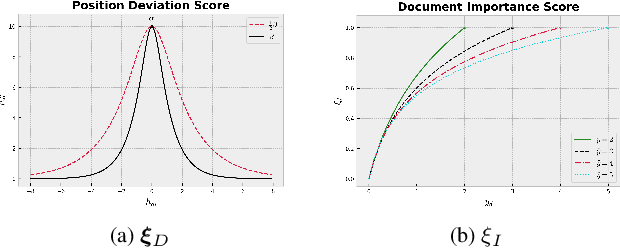
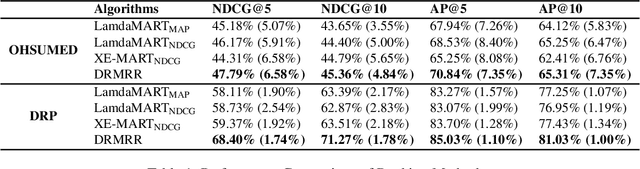
Despite their empirical success, most existing listwiselearning-to-rank (LTR) models are not built to be robust to errors in labeling or annotation, distributional data shift, or adversarial data perturbations. To fill this gap, we introduce a new listwise LTR model called Distributionally Robust Multi-output Regression Ranking (DRMRR). Different from existing methods, the scoring function of DRMRR was designed as a multivariate mapping from a feature vector to a vector of deviation scores, which captures local context information and cross-document interactions. DRMRR uses a Distributionally Robust Optimization (DRO) framework to minimize a multi-output loss function under the most adverse distributions in the neighborhood of the empirical data distribution defined by a Wasserstein ball. We show that this is equivalent to a regularized regression problem with a matrix norm regularizer. Our experiments were conducted on two real-world applications, medical document retrieval, and drug response prediction, showing that DRMRR notably outperforms state-of-the-art LTR models. We also conducted a comprehensive analysis to assess the resilience of DRMRR against various types of noise: Gaussian noise, adversarial perturbations, and label poisoning. We show that DRMRR is not only able to achieve significantly better performance than other baselines, but it can maintain a relatively stable performance as more noise is added to the data.

Distributionally Robust Multiclass Classification and Applications in Deep CNN Image Classifiers

We develop a Distributionally Robust Optimization (DRO) formulation for Multiclass Logistic Regression (MLR), which could tolerate data contaminated by outliers. The DRO framework uses a probabilistic ambiguity set defined as a ball of distributions that are close to the empirical distribution of the training set in the sense of the Wasserstein metric. We relax the DRO formulation into a regularized learning problem whose regularizer is a norm of the coefficient matrix. We establish out-of-sample performance guarantees for the solutions to our model, offering insights on the role of the regularizer in controlling the prediction error. We apply the proposed method in rendering deep CNN-based image classifiers robust to random and adversarial attacks. Specifically, using the MNIST and CIFAR-10 datasets, we demonstrate reductions in test error rate by up to 78.8% and loss by up to 90.8%. We also show that with a limited number of perturbed images in the training set, our method can improve the error rate by up to 49.49% and the loss by up to 68.93% compared to Empirical Risk Minimization (ERM), converging faster to an ideal loss/error rate as the number of perturbed images increases.

Provable Hierarchical Imitation Learning via EM

Due to recent empirical successes, the options framework for hierarchical reinforcement learning is gaining increasing popularity. Rather than learning from rewards which suffers from the curse of dimensionality, we consider learning an options-type hierarchical policy from expert demonstrations. Such a problem is referred to as hierarchical imitation learning. Converting this problem to parameter inference in a latent variable model, we theoretically characterize the EM approach proposed by Daniel et al. (2016). The population level algorithm is analyzed as an intermediate step, which is nontrivial due to the samples being correlated. If the expert policy can be parameterized by a variant of the options framework, then under regularity conditions, we prove that the proposed algorithm converges with high probability to a norm ball around the true parameter. To our knowledge, this is the first performance guarantee for an hierarchical imitation learning algorithm that only observes primitive state-action pairs.

Learning Optimal Personalized Treatment Rules Using Robust Regression Informed K-NN

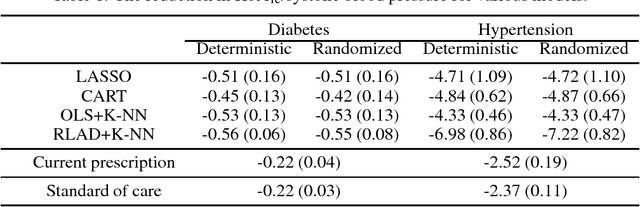
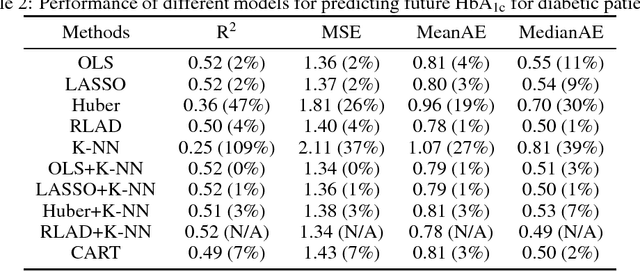
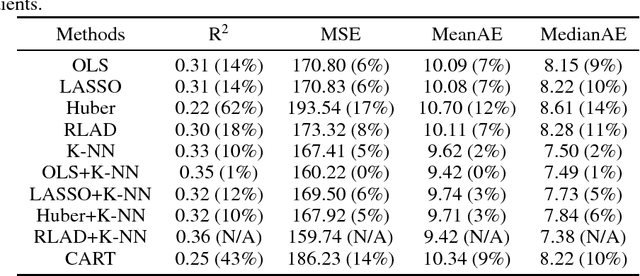
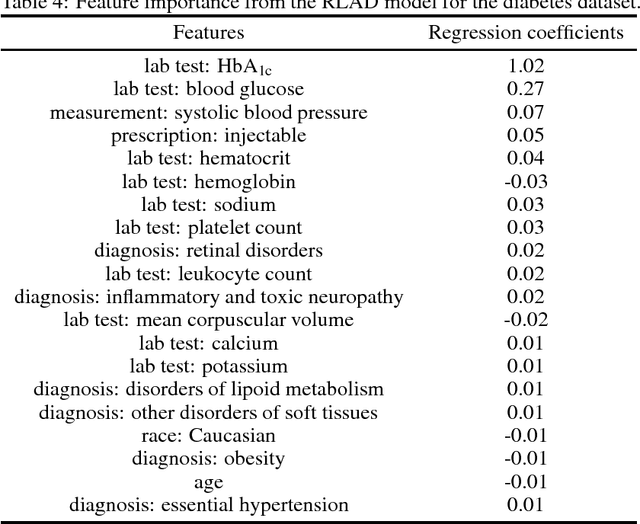
We develop a prediction-based prescriptive model for learning optimal personalized treatments for patients based on their Electronic Health Records (EHRs). Our approach consists of: (i) predicting future outcomes under each possible therapy using a robustified nonlinear model, and (ii) adopting a randomized prescriptive policy determined by the predicted outcomes. We show theoretical results that guarantee the out-of-sample predictive power of the model, and prove the optimality of the randomized strategy in terms of the expected true future outcome. We apply the proposed methodology to develop optimal therapies for patients with type 2 diabetes or hypertension using EHRs from a major safety-net hospital in New England, and show that our algorithm leads to a larger reduction of the HbA1c, for diabetics, or systolic blood pressure, for patients with hypertension, compared to the alternatives. We demonstrate that our approach outperforms the standard of care under the robustified nonlinear predictive model.

Sequential Dynamic Decision Making with Deep Neural Nets on a Test-Time Budget

Deep neural network (DNN) based approaches hold significant potential for reinforcement learning (RL) and have already shown remarkable gains over state-of-art methods in a number of applications. The effectiveness of DNN methods can be attributed to leveraging the abundance of supervised data to learn value functions, Q-functions, and policy function approximations without the need for feature engineering. Nevertheless, the deployment of DNN-based predictors with very deep architectures can pose an issue due to computational and other resource constraints at test-time in a number of applications. We propose a novel approach for reducing the average latency by learning a computationally efficient gating function that is capable of recognizing states in a sequential decision process for which policy prescriptions of a shallow network suffices and deeper layers of the DNN have little marginal utility. The overall system is adaptive in that it dynamically switches control actions based on state-estimates in order to reduce average latency without sacrificing terminal performance. We experiment with a number of alternative loss-functions to train gating functions and shallow policies and show that in a number of applications a speed-up of up to almost 5X can be obtained with little loss in performance.