Distributionally Robust Multiclass Classification and Applications in Deep Image Classifiers

We develop a Distributionally Robust Optimization (DRO) formulation for Multiclass Logistic Regression (MLR), which could tolerate data contaminated by outliers. The DRO framework uses a probabilistic ambiguity set defined as a ball of distributions that are close to the empirical distribution of the training set in the sense of the Wasserstein metric. We relax the DRO formulation into a regularized learning problem whose regularizer is a norm of the coefficient matrix. We establish out-of-sample performance guarantees for the solutions to our model, offering insights on the role of the regularizer in controlling the prediction error. We apply the proposed method in rendering deep Vision Transformer (ViT)-based image classifiers robust to random and adversarial attacks. Specifically, using the MNIST and CIFAR-10 datasets, we demonstrate reductions in test error rate by up to 83.5% and loss by up to 91.3% compared with baseline methods, by adopting a novel random training method.

Distributionally Robust Multi-Output Regression Ranking

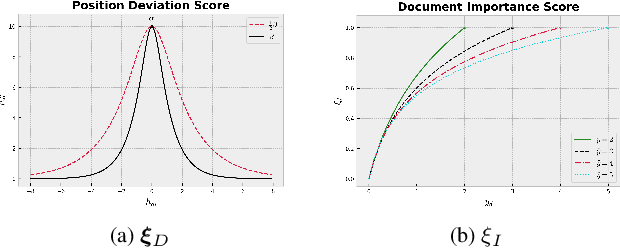
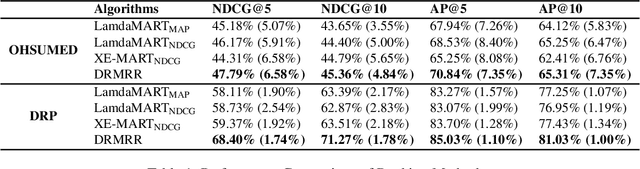
Despite their empirical success, most existing listwiselearning-to-rank (LTR) models are not built to be robust to errors in labeling or annotation, distributional data shift, or adversarial data perturbations. To fill this gap, we introduce a new listwise LTR model called Distributionally Robust Multi-output Regression Ranking (DRMRR). Different from existing methods, the scoring function of DRMRR was designed as a multivariate mapping from a feature vector to a vector of deviation scores, which captures local context information and cross-document interactions. DRMRR uses a Distributionally Robust Optimization (DRO) framework to minimize a multi-output loss function under the most adverse distributions in the neighborhood of the empirical data distribution defined by a Wasserstein ball. We show that this is equivalent to a regularized regression problem with a matrix norm regularizer. Our experiments were conducted on two real-world applications, medical document retrieval, and drug response prediction, showing that DRMRR notably outperforms state-of-the-art LTR models. We also conducted a comprehensive analysis to assess the resilience of DRMRR against various types of noise: Gaussian noise, adversarial perturbations, and label poisoning. We show that DRMRR is not only able to achieve significantly better performance than other baselines, but it can maintain a relatively stable performance as more noise is added to the data.

Distributionally Robust Multiclass Classification and Applications in Deep CNN Image Classifiers

We develop a Distributionally Robust Optimization (DRO) formulation for Multiclass Logistic Regression (MLR), which could tolerate data contaminated by outliers. The DRO framework uses a probabilistic ambiguity set defined as a ball of distributions that are close to the empirical distribution of the training set in the sense of the Wasserstein metric. We relax the DRO formulation into a regularized learning problem whose regularizer is a norm of the coefficient matrix. We establish out-of-sample performance guarantees for the solutions to our model, offering insights on the role of the regularizer in controlling the prediction error. We apply the proposed method in rendering deep CNN-based image classifiers robust to random and adversarial attacks. Specifically, using the MNIST and CIFAR-10 datasets, we demonstrate reductions in test error rate by up to 78.8% and loss by up to 90.8%. We also show that with a limited number of perturbed images in the training set, our method can improve the error rate by up to 49.49% and the loss by up to 68.93% compared to Empirical Risk Minimization (ERM), converging faster to an ideal loss/error rate as the number of perturbed images increases.

Distributionally Robust Learning

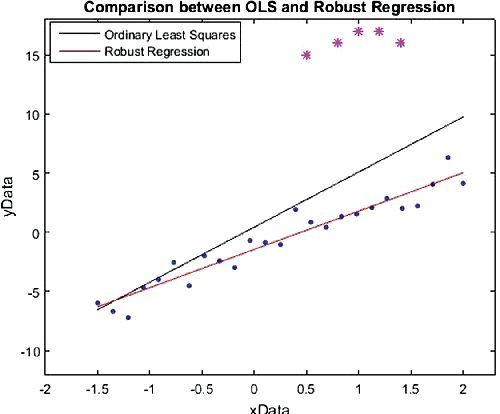
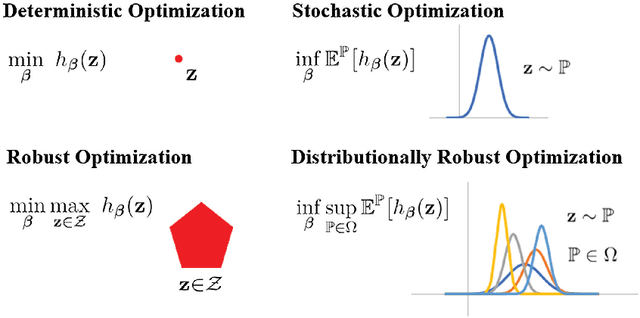
This monograph develops a comprehensive statistical learning framework that is robust to (distributional) perturbations in the data using Distributionally Robust Optimization (DRO) under the Wasserstein metric. Beginning with fundamental properties of the Wasserstein metric and the DRO formulation, we explore duality to arrive at tractable formulations and develop finite-sample, as well as asymptotic, performance guarantees. We consider a series of learning problems, including (i) distributionally robust linear regression; (ii) distributionally robust regression with group structure in the predictors; (iii) distributionally robust multi-output regression and multiclass classification, (iv) optimal decision making that combines distributionally robust regression with nearest-neighbor estimation; (v) distributionally robust semi-supervised learning, and (vi) distributionally robust reinforcement learning. A tractable DRO relaxation for each problem is being derived, establishing a connection between robustness and regularization, and obtaining bounds on the prediction and estimation errors of the solution. Beyond theory, we include numerical experiments and case studies using synthetic and real data. The real data experiments are all associated with various health informatics problems, an application area which provided the initial impetus for this work.

Robust Grouped Variable Selection Using Distributionally Robust Optimization

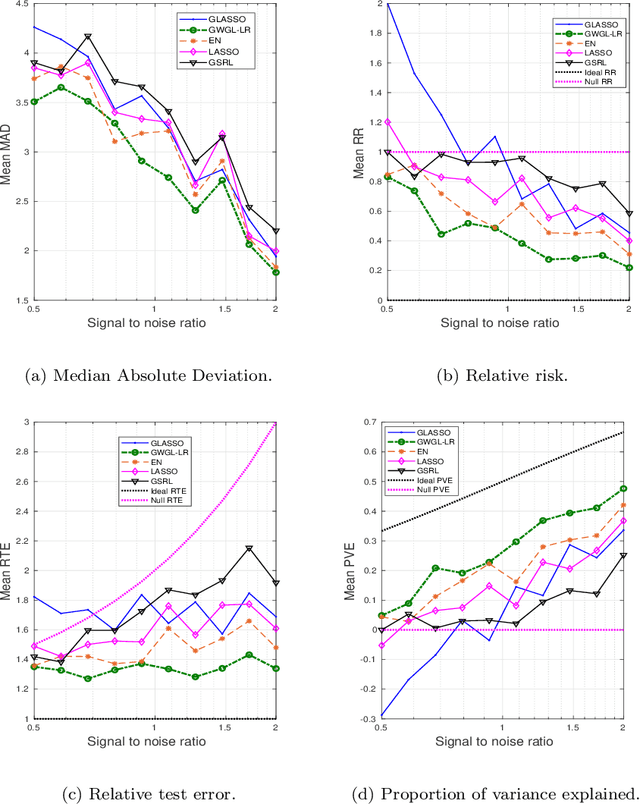
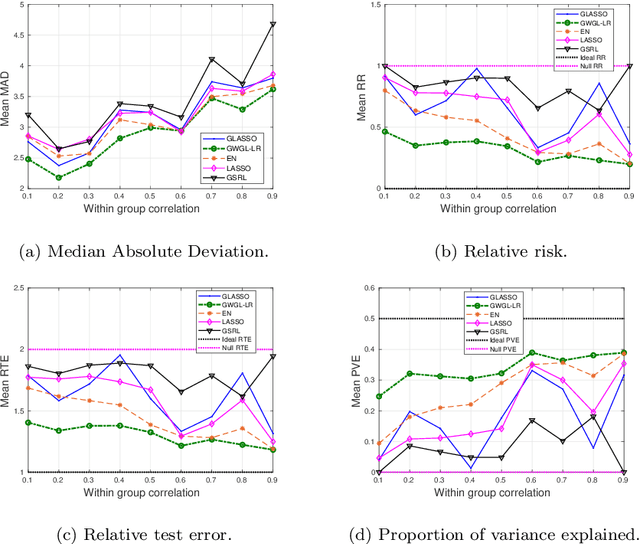
We propose a Distributionally Robust Optimization (DRO) formulation with a Wasserstein-based uncertainty set for selecting grouped variables under perturbations on the data for both linear regression and classification problems. The resulting model offers robustness explanations for Grouped Least Absolute Shrinkage and Selection Operator (GLASSO) algorithms and highlights the connection between robustness and regularization. We prove probabilistic bounds on the out-of-sample loss and the estimation bias, and establish the grouping effect of our estimator, showing that coefficients in the same group converge to the same value as the sample correlation between covariates approaches 1. Based on this result, we propose to use the spectral clustering algorithm with the Gaussian similarity function to perform grouping on the predictors, which makes our approach applicable without knowing the grouping structure a priori. We compare our approach to an array of alternatives and provide extensive numerical results on both synthetic data and a real large dataset of surgery-related medical records, showing that our formulation produces an interpretable and parsimonious model that encourages sparsity at a group level and is able to achieve better prediction and estimation performance in the presence of outliers.

Robustified Multivariate Regression and Classification Using Distributionally Robust Optimization under the Wasserstein Metric

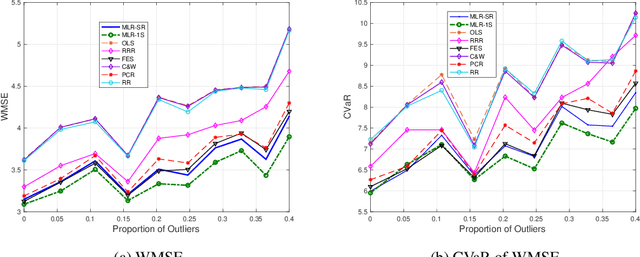
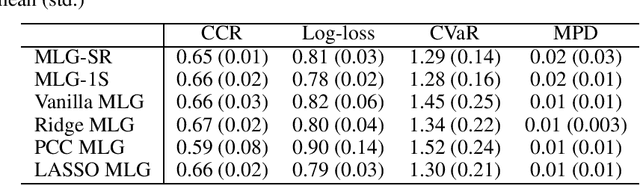
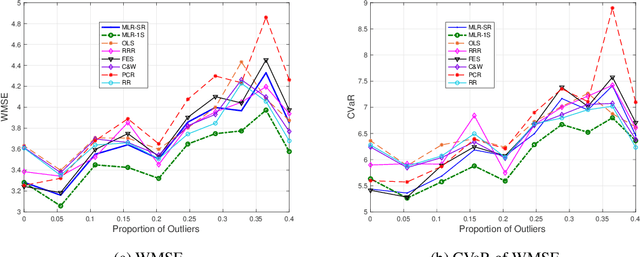
We develop Distributionally Robust Optimization (DRO) formulations for Multivariate Linear Regression (MLR) and Multiclass Logistic Regression (MLG) when both the covariates and responses/labels may be contaminated by outliers. The DRO framework uses a probabilistic ambiguity set defined as a ball of distributions that are close to the empirical distribution of the training set in the sense of the Wasserstein metric. We relax the DRO formulation into a regularized learning problem whose regularizer is a norm of the coefficient matrix. We establish out-of-sample performance guarantees for the solutions to our model, offering insights on the role of the regularizer in controlling the prediction error. Experimental results show that our approach improves the predictive error by 7% -- 37% for MLR, and a metric of robustness by 100% for MLG.

Learning Optimal Personalized Treatment Rules Using Robust Regression Informed K-NN

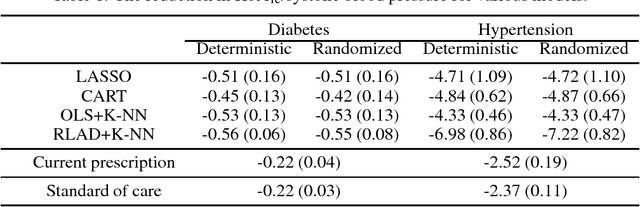
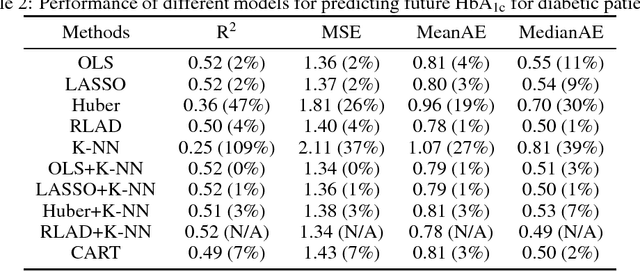
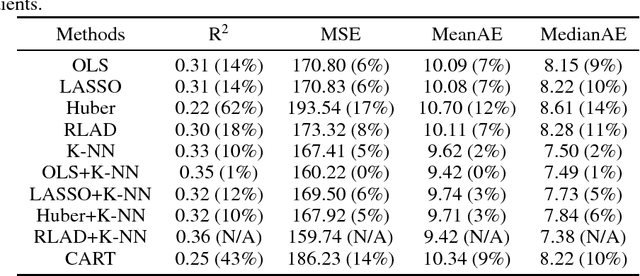
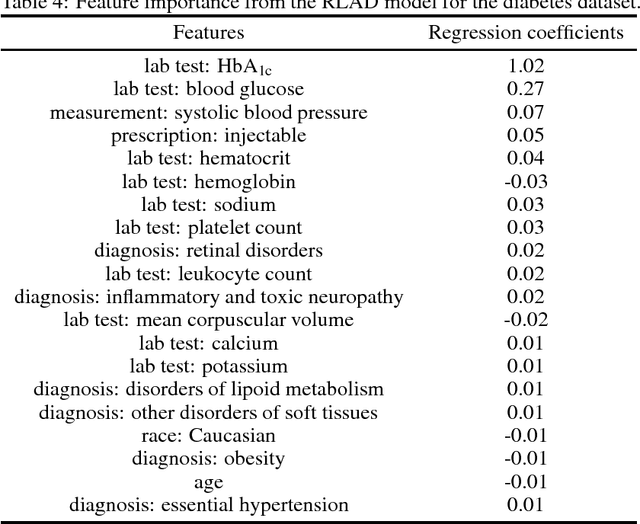
We develop a prediction-based prescriptive model for learning optimal personalized treatments for patients based on their Electronic Health Records (EHRs). Our approach consists of: (i) predicting future outcomes under each possible therapy using a robustified nonlinear model, and (ii) adopting a randomized prescriptive policy determined by the predicted outcomes. We show theoretical results that guarantee the out-of-sample predictive power of the model, and prove the optimality of the randomized strategy in terms of the expected true future outcome. We apply the proposed methodology to develop optimal therapies for patients with type 2 diabetes or hypertension using EHRs from a major safety-net hospital in New England, and show that our algorithm leads to a larger reduction of the HbA1c, for diabetics, or systolic blood pressure, for patients with hypertension, compared to the alternatives. We demonstrate that our approach outperforms the standard of care under the robustified nonlinear predictive model.

A Robust Learning Algorithm for Regression Models Using Distributionally Robust Optimization under the Wasserstein Metric

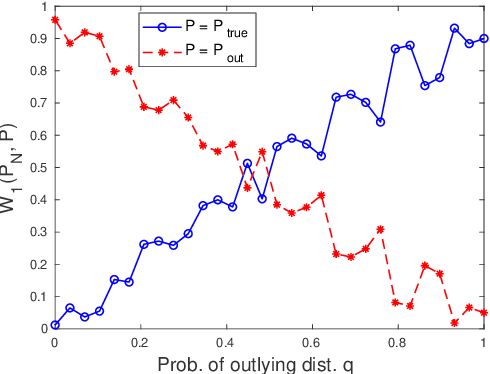
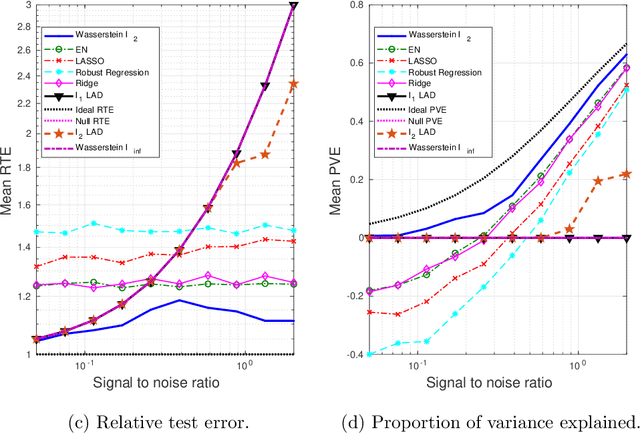
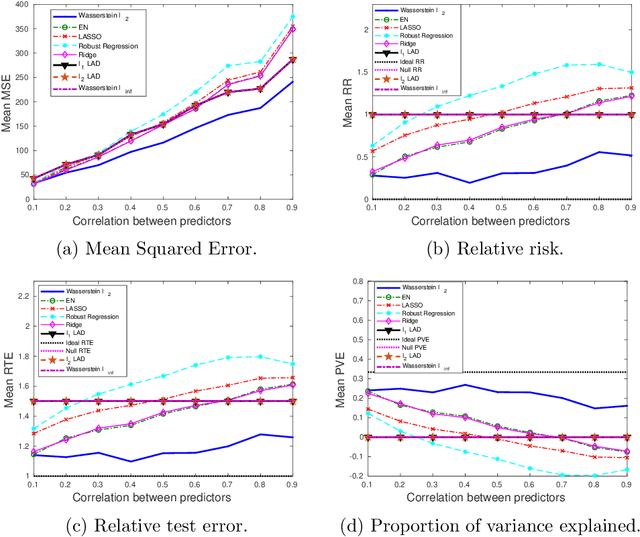
We present a Distributionally Robust Optimization (DRO) approach to estimate a robustified regression plane in a linear regression setting, when the observed samples are potentially contaminated with adversarially corrupted outliers. Our approach mitigates the impact of outliers through hedging against a family of distributions on the observed data, some of which assign very low probabilities to the outliers. The set of distributions under consideration are close to the empirical distribution in the sense of the Wasserstein metric. We show that this DRO formulation can be relaxed to a convex optimization problem which encompasses a class of models. By selecting proper norm spaces for the Wasserstein metric, we are able to recover several commonly used regularized regression models. We provide new insights into the regularization term and give guidance on the selection of the regularization coefficient from the standpoint of a confidence region. We establish two types of performance guarantees for the solution to our formulation under mild conditions. One is related to its out-of-sample behavior (prediction bias), and the other concerns the discrepancy between the estimated and true regression planes (estimation bias). Extensive numerical results demonstrate the superiority of our approach to a host of regression models, in terms of the prediction and estimation accuracies. We also consider the application of our robust learning procedure to outlier detection, and show that our approach achieves a much higher AUC (Area Under the ROC Curve) than M-estimation.