A Robust Learning Algorithm for Regression Models Using Distributionally Robust Optimization under the Wasserstein Metric
Paper and Code
May 10, 2018
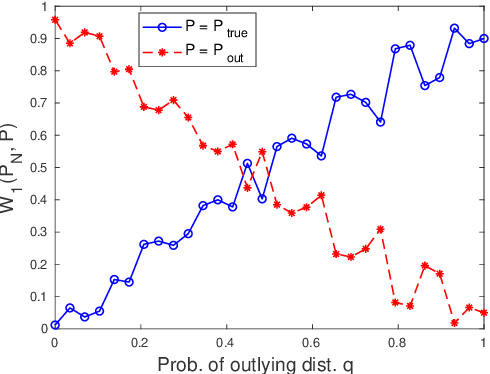
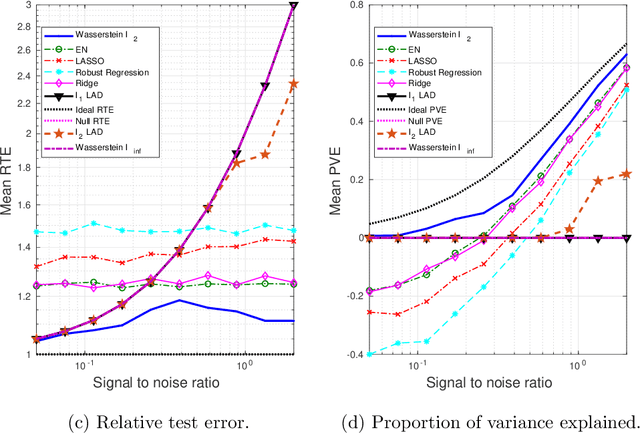
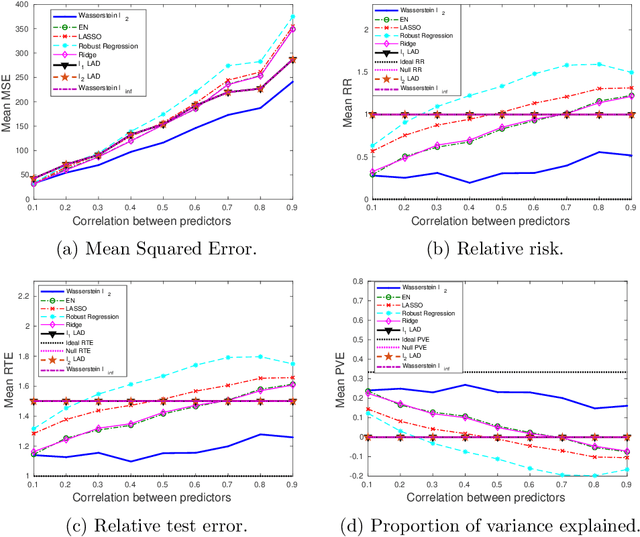
We present a Distributionally Robust Optimization (DRO) approach to estimate a robustified regression plane in a linear regression setting, when the observed samples are potentially contaminated with adversarially corrupted outliers. Our approach mitigates the impact of outliers through hedging against a family of distributions on the observed data, some of which assign very low probabilities to the outliers. The set of distributions under consideration are close to the empirical distribution in the sense of the Wasserstein metric. We show that this DRO formulation can be relaxed to a convex optimization problem which encompasses a class of models. By selecting proper norm spaces for the Wasserstein metric, we are able to recover several commonly used regularized regression models. We provide new insights into the regularization term and give guidance on the selection of the regularization coefficient from the standpoint of a confidence region. We establish two types of performance guarantees for the solution to our formulation under mild conditions. One is related to its out-of-sample behavior (prediction bias), and the other concerns the discrepancy between the estimated and true regression planes (estimation bias). Extensive numerical results demonstrate the superiority of our approach to a host of regression models, in terms of the prediction and estimation accuracies. We also consider the application of our robust learning procedure to outlier detection, and show that our approach achieves a much higher AUC (Area Under the ROC Curve) than M-estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge