Game-theoretic Counterfactual Explanation for Graph Neural Networks

Graph Neural Networks (GNNs) have been a powerful tool for node classification tasks in complex networks. However, their decision-making processes remain a black-box to users, making it challenging to understand the reasoning behind their predictions. Counterfactual explanations (CFE) have shown promise in enhancing the interpretability of machine learning models. Prior approaches to compute CFE for GNNS often are learning-based approaches that require training additional graphs. In this paper, we propose a semivalue-based, non-learning approach to generate CFE for node classification tasks, eliminating the need for any additional training. Our results reveals that computing Banzhaf values requires lower sample complexity in identifying the counterfactual explanations compared to other popular methods such as computing Shapley values. Our empirical evidence indicates computing Banzhaf values can achieve up to a fourfold speed up compared to Shapley values. We also design a thresholding method for computing Banzhaf values and show theoretical and empirical results on its robustness in noisy environments, making it superior to Shapley values. Furthermore, the thresholded Banzhaf values are shown to enhance efficiency without compromising the quality (i.e., fidelity) in the explanations in three popular graph datasets.

Slowly Changing Adversarial Bandit Algorithms are Provably Efficient for Discounted MDPs

Reinforcement learning (RL) generalizes bandit problems with additional difficulties on longer planning horzion and unknown transition kernel. We show that, under some mild assumptions, \textbf{any} slowly changing adversarial bandit algorithm enjoys near-optimal regret in adversarial bandits can achieve near-optimal (expected) regret in non-episodic discounted MDPs. The slowly changing property required by our generalization is mild, see e.g. (Even-Dar et al. 2009, Neu et al. 2010), we also show, for example, \expt~(Auer et al. 2002) is slowly changing and enjoys near-optimal regret in MDPs.

Fair Decision-Making for Food Inspections

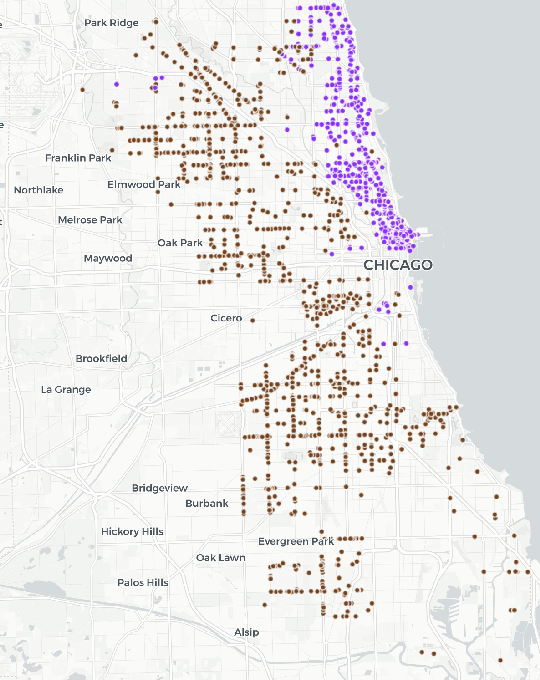
We revisit the application of predictive models by the Chicago Department of Public Health to schedule restaurant inspections and prioritize the detection of critical violations of the food code. Performing the first analysis from the perspective of fairness to the population served by the restaurants, we find that the model treats inspections unequally based on the sanitarian who conducted the inspection and that in turn there are both geographic and demographic disparities in the benefits of the model. We examine both approaches to use the original model in a fairer way and ways to train the model to achieve fairness and find more success with the former class of approaches. The challenges from this application point to important directions for future work around fairness with collective entities rather than individuals, the use of critical violations as a proxy, and the disconnect between fair classification and fairness in the dynamic scheduling system.

Combining No-regret and Q-learning

Counterfactual Regret Minimization (CFR) has found success in settings like poker which have both terminal states and perfect recall. We seek to understand how to relax these requirements. As a first step, we introduce a simple algorithm, local no-regret learning (LONR), which uses a Q-learning-like update rule to allow learning without terminal states or perfect recall. We prove its convergence for the basic case of MDPs (and limited extensions of them) and present empirical results showing that it achieves last iterate convergence in a number of settings, most notably NoSDE games, a class of Markov games specifically designed to be challenging to learn where no prior algorithm is known to achieve convergence to a stationary equilibrium even on average.

Elicitation Complexity of Statistical Properties

A property, or statistical functional, is said to be elicitable if it minimizes expected loss for some loss function. The study of which properties are elicitable sheds light on the capabilities and limits of empirical risk minimization. While several recent papers have asked which properties are elicitable, we instead advocate for a more nuanced question: how many dimensions are required to indirectly elicit a given property? This number is called the elicitation complexity of the property. We lay the foundation for a general theory of elicitation complexity, including several basic results about how elicitation complexity behaves, and the complexity of standard properties of interest. Building on this foundation, we establish several upper and lower bounds for the broad class of Bayes risks. We apply these results by proving tight complexity bounds, with respect to identifiable properties, for variance, financial risk measures, entropy, norms, and new properties of interest. We then show how some of these bounds can extend to other practical classes of properties, and conclude with a discussion of open directions.

Multiagent Learning in Large Anonymous Games

In large systems, it is important for agents to learn to act effectively, but sophisticated multi-agent learning algorithms generally do not scale. An alternative approach is to find restricted classes of games where simple, efficient algorithms converge. It is shown that stage learning efficiently converges to Nash equilibria in large anonymous games if best-reply dynamics converge. Two features are identified that improve convergence. First, rather than making learning more difficult, more agents are actually beneficial in many settings. Second, providing agents with statistical information about the behavior of others can significantly reduce the number of observations needed.