On Measuring Unnoticeability of Graph Adversarial Attacks: Observations, New Measure, and Applications

Adversarial attacks are allegedly unnoticeable. Prior studies have designed attack noticeability measures on graphs, primarily using statistical tests to compare the topology of original and (possibly) attacked graphs. However, we observe two critical limitations in the existing measures. First, because the measures rely on simple rules, attackers can readily enhance their attacks to bypass them, reducing their attack "noticeability" and, yet, maintaining their attack performance. Second, because the measures naively leverage global statistics, such as degree distributions, they may entirely overlook attacks until severe perturbations occur, letting the attacks be almost "totally unnoticeable." To address the limitations, we introduce HideNSeek, a learnable measure for graph attack noticeability. First, to mitigate the bypass problem, HideNSeek learns to distinguish the original and (potential) attack edges using a learnable edge scorer (LEO), which scores each edge on its likelihood of being an attack. Second, to mitigate the overlooking problem, HideNSeek conducts imbalance-aware aggregation of all the edge scores to obtain the final noticeability score. Using six real-world graphs, we empirically demonstrate that HideNSeek effectively alleviates the observed limitations, and LEO (i.e., our learnable edge scorer) outperforms eleven competitors in distinguishing attack edges under five different attack methods. For an additional application, we show that LEO boost the performance of robust GNNs by removing attack-like edges.

Tackling Prevalent Conditions in Unsupervised Combinatorial Optimization: Cardinality, Minimum, Covering, and More

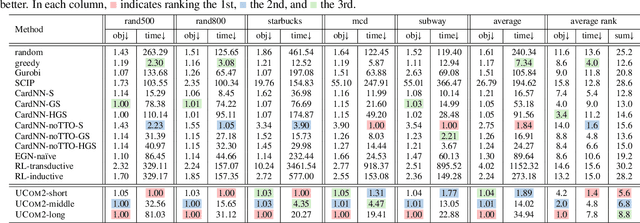
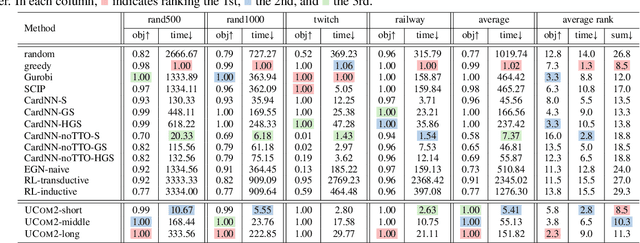
Combinatorial optimization (CO) is naturally discrete, making machine learning based on differentiable optimization inapplicable. Karalias & Loukas (2020) adapted the probabilistic method to incorporate CO into differentiable optimization. Their work ignited the research on unsupervised learning for CO, composed of two main components: probabilistic objectives and derandomization. However, each component confronts unique challenges. First, deriving objectives under various conditions (e.g., cardinality constraints and minimum) is nontrivial. Second, the derandomization process is underexplored, and the existing derandomization methods are either random sampling or naive rounding. In this work, we aim to tackle prevalent (i.e., commonly involved) conditions in unsupervised CO. First, we concretize the targets for objective construction and derandomization with theoretical justification. Then, for various conditions commonly involved in different CO problems, we derive nontrivial objectives and derandomization to meet the targets. Finally, we apply the derivations to various CO problems. Via extensive experiments on synthetic and real-world graphs, we validate the correctness of our derivations and show our empirical superiority w.r.t. both optimization quality and speed.

Robust Graph Clustering via Meta Weighting for Noisy Graphs

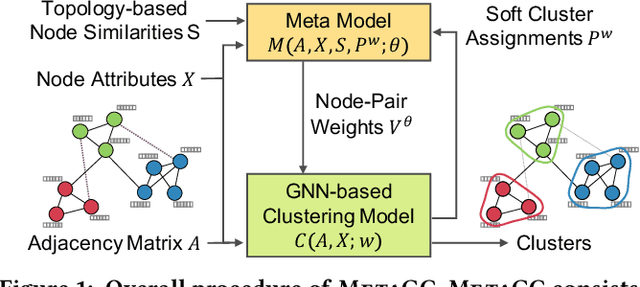
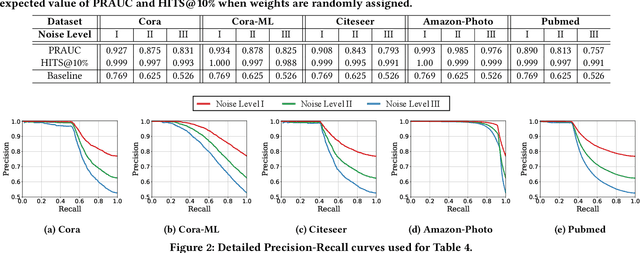
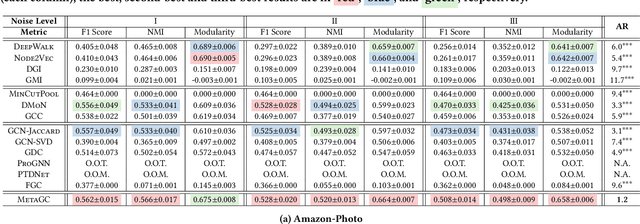
How can we find meaningful clusters in a graph robustly against noise edges? Graph clustering (i.e., dividing nodes into groups of similar ones) is a fundamental problem in graph analysis with applications in various fields. Recent studies have demonstrated that graph neural network (GNN) based approaches yield promising results for graph clustering. However, we observe that their performance degenerates significantly on graphs with noise edges, which are prevalent in practice. In this work, we propose MetaGC for robust GNN-based graph clustering. MetaGC employs a decomposable clustering loss function, which can be rephrased as a sum of losses over node pairs. We add a learnable weight to each node pair, and MetaGC adaptively adjusts the weights of node pairs using meta-weighting so that the weights of meaningful node pairs increase and the weights of less-meaningful ones (e.g., noise edges) decrease. We show empirically that MetaGC learns weights as intended and consequently outperforms the state-of-the-art GNN-based competitors, even when they are equipped with separate denoising schemes, on five real-world graphs under varying levels of noise. Our code and datasets are available at https://github.com/HyeonsooJo/MetaGC.