Multilevel Clustering via Wasserstein Means

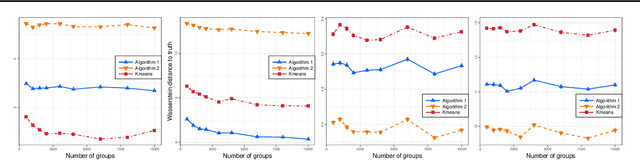
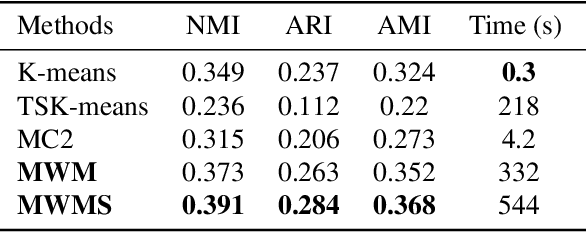
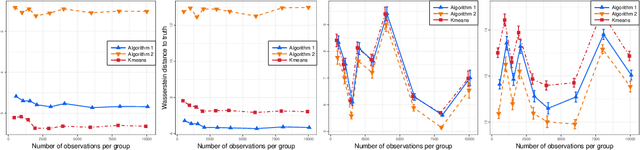
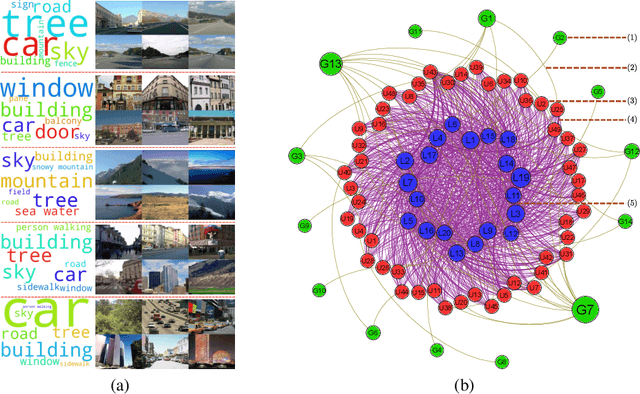
We propose a novel approach to the problem of multilevel clustering, which aims to simultaneously partition data in each group and discover grouping patterns among groups in a potentially large hierarchically structured corpus of data. Our method involves a joint optimization formulation over several spaces of discrete probability measures, which are endowed with Wasserstein distance metrics. We propose a number of variants of this problem, which admit fast optimization algorithms, by exploiting the connection to the problem of finding Wasserstein barycenters. Consistency properties are established for the estimates of both local and global clusters. Finally, experiment results with both synthetic and real data are presented to demonstrate the flexibility and scalability of the proposed approach.

Lifted Tree-Reweighted Variational Inference

We analyze variational inference for highly symmetric graphical models such as those arising from first-order probabilistic models. We first show that for these graphical models, the tree-reweighted variational objective lends itself to a compact lifted formulation which can be solved much more efficiently than the standard TRW formulation for the ground graphical model. Compared to earlier work on lifted belief propagation, our formulation leads to a convex optimization problem for lifted marginal inference and provides an upper bound on the partition function. We provide two approaches for improving the lifted TRW upper bound. The first is a method for efficiently computing maximum spanning trees in highly symmetric graphs, which can be used to optimize the TRW edge appearance probabilities. The second is a method for tightening the relaxation of the marginal polytope using lifted cycle inequalities and novel exchangeable cluster consistency constraints.

Bayesian Nonparametric Multilevel Clustering with Group-Level Contexts

We present a Bayesian nonparametric framework for multilevel clustering which utilizes group-level context information to simultaneously discover low-dimensional structures of the group contents and partitions groups into clusters. Using the Dirichlet process as the building block, our model constructs a product base-measure with a nested structure to accommodate content and context observations at multiple levels. The proposed model possesses properties that link the nested Dirichlet processes (nDP) and the Dirichlet process mixture models (DPM) in an interesting way: integrating out all contents results in the DPM over contexts, whereas integrating out group-specific contexts results in the nDP mixture over content variables. We provide a Polya-urn view of the model and an efficient collapsed Gibbs inference procedure. Extensive experiments on real-world datasets demonstrate the advantage of utilizing context information via our model in both text and image domains.