Multilevel Clustering via Wasserstein Means
Paper and Code
Jun 13, 2017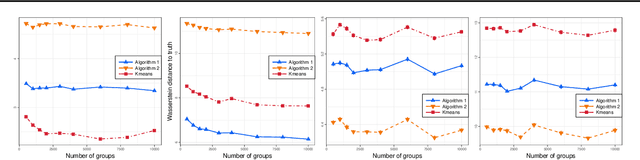
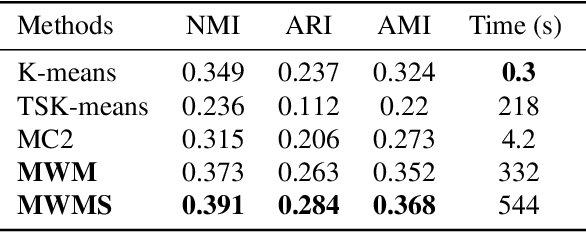
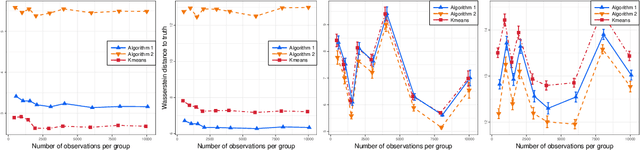
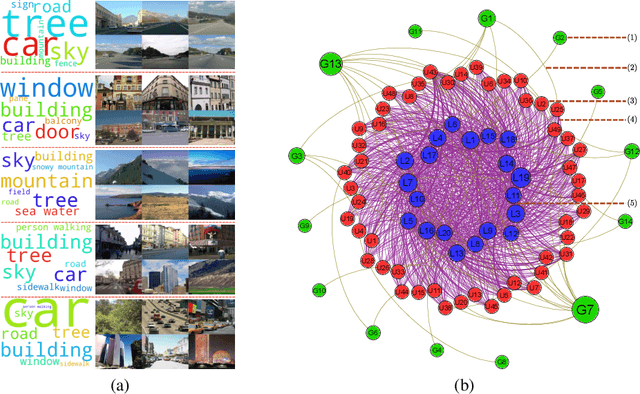
We propose a novel approach to the problem of multilevel clustering, which aims to simultaneously partition data in each group and discover grouping patterns among groups in a potentially large hierarchically structured corpus of data. Our method involves a joint optimization formulation over several spaces of discrete probability measures, which are endowed with Wasserstein distance metrics. We propose a number of variants of this problem, which admit fast optimization algorithms, by exploiting the connection to the problem of finding Wasserstein barycenters. Consistency properties are established for the estimates of both local and global clusters. Finally, experiment results with both synthetic and real data are presented to demonstrate the flexibility and scalability of the proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge