CLERF: Contrastive LEaRning for Full Range Head Pose Estimation

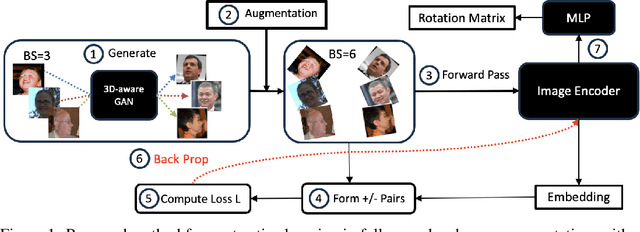
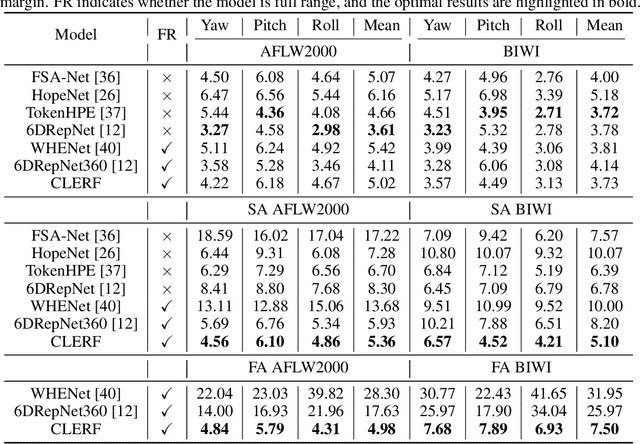
We introduce a novel framework for representation learning in head pose estimation (HPE). Previously such a scheme was difficult due to head pose data sparsity, making triplet sampling infeasible. Recent progress in 3D generative adversarial networks (3D-aware GAN) has opened the door for easily sampling triplets (anchor, positive, negative). We perform contrastive learning on extensively augmented data including geometric transformations and demonstrate that contrastive learning allows networks to learn genuine features that contribute to accurate HPE. On the other hand, we observe that existing HPE works struggle to predict head poses as accurately when test image rotation matrices are slightly out of the training dataset distribution. Experiments show that our methodology performs on par with state-of-the-art models on standard test datasets and outperforms them when images are slightly rotated/ flipped or full range head pose. To the best of our knowledge, we are the first to deliver a true full range HPE model capable of accurately predicting any head pose including upside-down pose. Furthermore, we compared with other existing full-yaw range models and demonstrated superior results.

Full-range Head Pose Geometric Data Augmentations

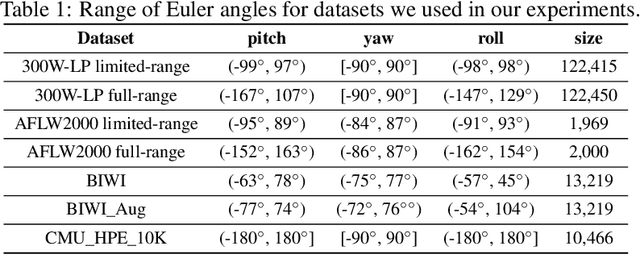
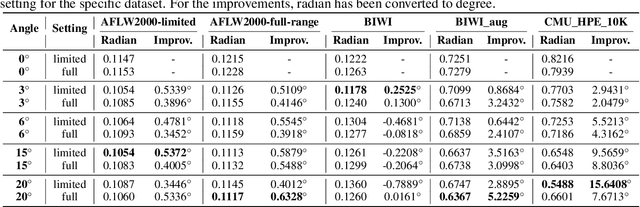
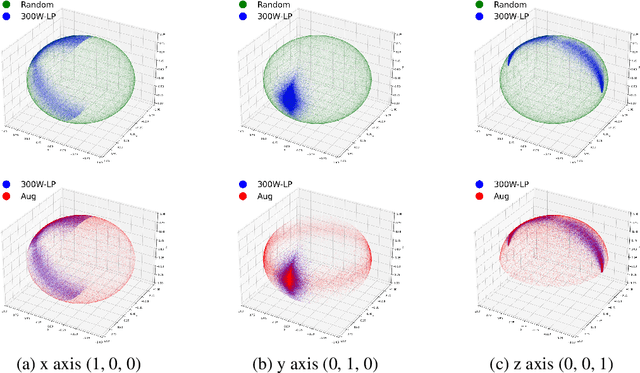
Many head pose estimation (HPE) methods promise the ability to create full-range datasets, theoretically allowing the estimation of the rotation and positioning of the head from various angles. However, these methods are only accurate within a range of head angles; exceeding this specific range led to significant inaccuracies. This is dominantly explained by unclear specificity of the coordinate systems and Euler Angles used in the foundational rotation matrix calculations. Here, we addressed these limitations by presenting (1) methods that accurately infer the correct coordinate system and Euler angles in the correct axis-sequence, (2) novel formulae for 2D geometric augmentations of the rotation matrices under the (SPECIFIC) coordinate system, (3) derivations for the correct drawing routines for rotation matrices and poses, and (4) mathematical experimentation and verification that allow proper pitch-yaw coverage for full-range head pose dataset generation. Performing our augmentation techniques to existing head pose estimation methods demonstrated a significant improvement to the model performance. Code will be released upon paper acceptance.

Mathematical Foundation and Corrections for Full Range Head Pose Estimation

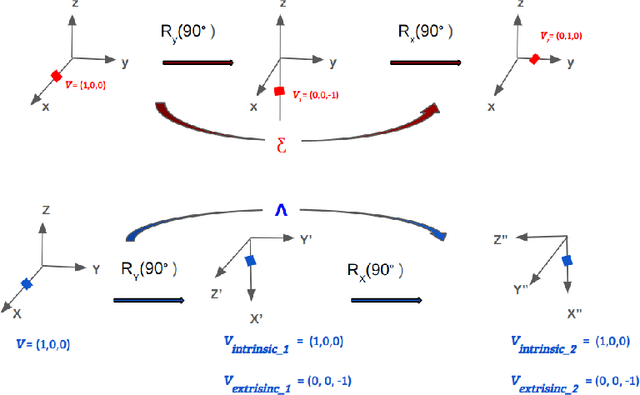
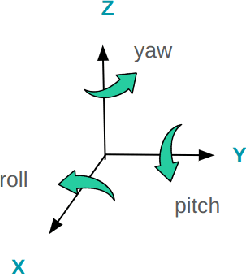
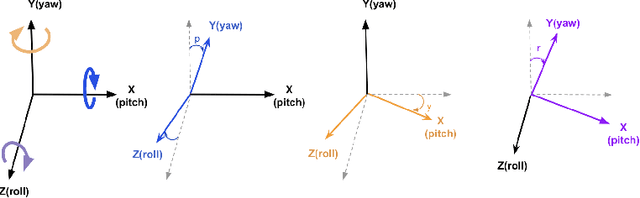
Numerous works concerning head pose estimation (HPE) offer algorithms or proposed neural network-based approaches for extracting Euler angles from either facial key points or directly from images of the head region. However, many works failed to provide clear definitions of the coordinate systems and Euler or Tait-Bryan angles orders in use. It is a well-known fact that rotation matrices depend on coordinate systems, and yaw, roll, and pitch angles are sensitive to their application order. Without precise definitions, it becomes challenging to validate the correctness of the output head pose and drawing routines employed in prior works. In this paper, we thoroughly examined the Euler angles defined in the 300W-LP dataset, head pose estimation such as 3DDFA-v2, 6D-RepNet, WHENet, etc, and the validity of their drawing routines of the Euler angles. When necessary, we infer their coordinate system and sequence of yaw, roll, pitch from provided code. This paper presents (1) code and algorithms for inferring coordinate system from provided source code, code for Euler angle application order and extracting precise rotation matrices and the Euler angles, (2) code and algorithms for converting poses from one rotation system to another, (3) novel formulae for 2D augmentations of the rotation matrices, and (4) derivations and code for the correct drawing routines for rotation matrices and poses. This paper also addresses the feasibility of defining rotations with right-handed coordinate system in Wikipedia and SciPy, which makes the Euler angle extraction much easier for full-range head pose research.