Visible Light Positioning With Lamé Curve LEDs: A Generic Approach for Camera Pose Estimation

Camera-based visible light positioning (VLP) is a promising technique for accurate and low-cost indoor camera pose estimation (CPE). To reduce the number of required light-emitting diodes (LEDs), advanced methods commonly exploit LED shape features for positioning. Although interesting, they are typically restricted to a single LED geometry, leading to failure in heterogeneous LED-shape scenarios. To address this challenge, this paper investigates Lamé curves as a unified representation of common LED shapes and proposes a generic VLP algorithm using Lamé curve-shaped LEDs, termed LC-VLP. In the considered system, multiple ceiling-mounted Lamé curve-shaped LEDs periodically broadcast their curve parameters via visible light communication, which are captured by a camera-equipped receiver. Based on the received LED images and curve parameters, the receiver can estimate the camera pose using LC-VLP. Specifically, an LED database is constructed offline to store the curve parameters, while online positioning is formulated as a nonlinear least-squares problem and solved iteratively. To provide a reliable initialization, a correspondence-free perspective-\textit{n}-points (FreeP\textit{n}P) algorithm is further developed, enabling approximate CPE without any pre-calibrated reference points. The performance of LC-VLP is verified by both simulations and experiments. Simulations show that LC-VLP outperforms state-of-the-art methods in both circular- and rectangular-LED scenarios, achieving reductions of over 40% in position error and 25% in rotation error. Experiments further show that LC-VLP can achieve an average position accuracy of less than 4 cm.

Compressed domain vibration detection and classification for distributed acoustic sensing

Distributed acoustic sensing (DAS) is a novel enabling technology that can turn existing fibre optic networks to distributed acoustic sensors. However, it faces the challenges of transmitting, storing, and processing massive streams of data which are orders of magnitude larger than that collected from point sensors. The gap between intensive data generated by DAS and modern computing system with limited reading/writing speed and storage capacity imposes restrictions on many applications. Compressive sensing (CS) is a revolutionary signal acquisition method that allows a signal to be acquired and reconstructed with significantly fewer samples than that required by Nyquist-Shannon theorem. Though the data size is greatly reduced in the sampling stage, the reconstruction of the compressed data is however time and computation consuming. To address this challenge, we propose to map the feature extractor from Nyquist-domain to compressed-domain and therefore vibration detection and classification can be directly implemented in compressed-domain. The measured results show that our framework can be used to reduce the transmitted data size by 70% while achieves 99.4% true positive rate (TPR) and 0.04% false positive rate (TPR) along 5 km sensing fibre and 95.05% classification accuracy on a 5-class classification task.

Stable and Compact Face Recognition via Unlabeled Data Driven Sparse Representation-Based Classification

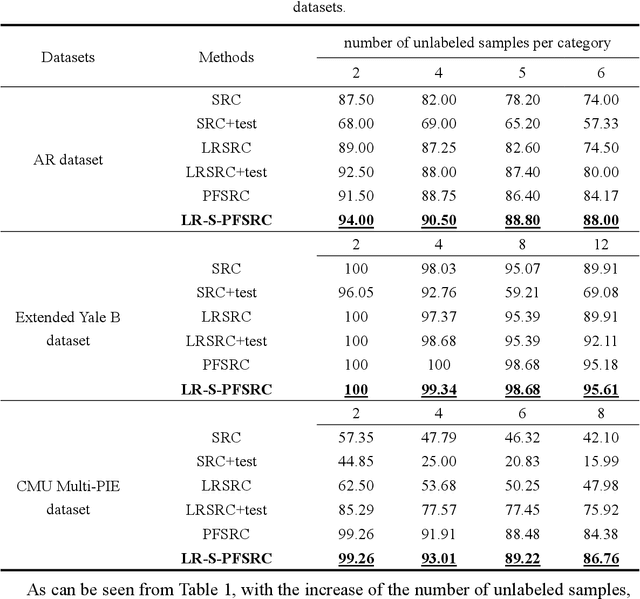
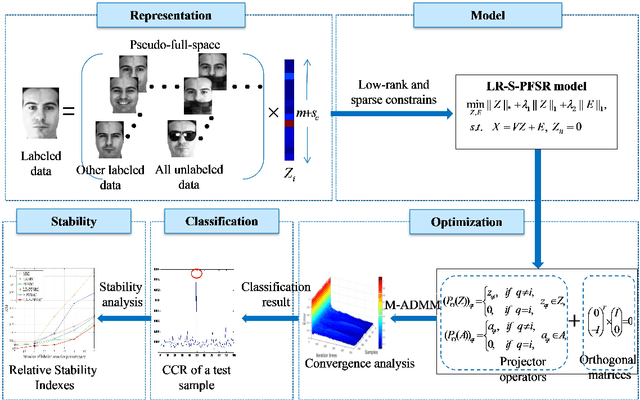
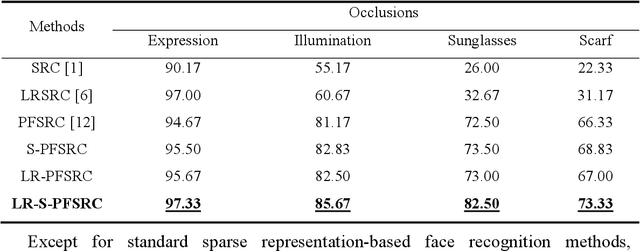
Sparse representation-based classification (SRC) has attracted much attention by casting the recognition problem as simple linear regression problem. SRC methods, however, still is limited to enough labeled samples per category, insufficient use of unlabeled samples, and instability of representation. For tackling these problems, an unlabeled data driven inverse projection pseudo-full-space representation-based classification model is proposed with low-rank sparse constraints. The proposed model aims to mine the hidden semantic information and intrinsic structure information of all available data, which is suitable for few labeled samples and proportion imbalance between labeled samples and unlabeled samples problems in frontal face recognition. The mixed Gauss-Seidel and Jacobian ADMM algorithm is introduced to solve the model. The convergence, representation capability and stability of the model are analyzed. Experiments on three public datasets show that the proposed LR-S-PFSRC model achieves stable results, especially for proportion imbalance of samples.