Bayesian Learning to Discover Mathematical Operations in Governing Equations of Dynamic Systems

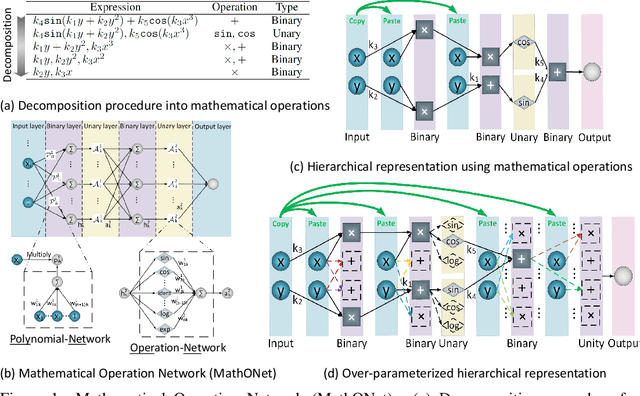
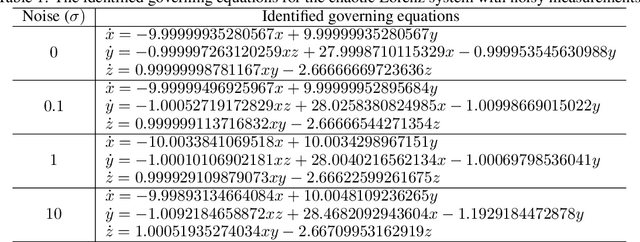
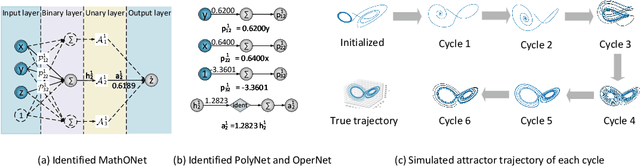
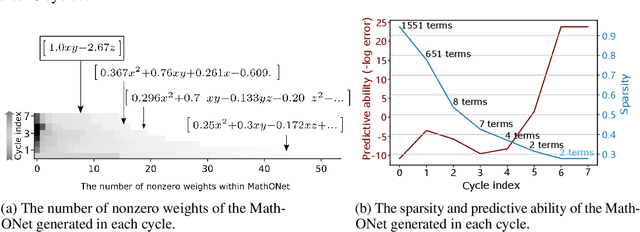
Discovering governing equations from data is critical for diverse scientific disciplines as they can provide insights into the underlying phenomenon of dynamic systems. This work presents a new representation for governing equations by designing the Mathematical Operation Network (MathONet) with a deep neural network-like hierarchical structure. Specifically, the MathONet is stacked by several layers of unary operations (e.g., sin, cos, log) and binary operations (e.g., +,-), respectively. An initialized MathONet is typically regarded as a super-graph with a redundant structure, a sub-graph of which can yield the governing equation. We develop a sparse group Bayesian learning algorithm to extract the sub-graph by employing structurally constructed priors over the redundant mathematical operations. By demonstrating the chaotic Lorenz system, Lotka-Volterra system, and Kolmogorov-Petrovsky-Piskunov system, the proposed method can discover the ordinary differential equations (ODEs) and partial differential equations (PDEs) from the observations given limited mathematical operations, without any prior knowledge on possible expressions of the ODEs and PDEs.

Sparse Bayesian Deep Learning for Dynamic System Identification

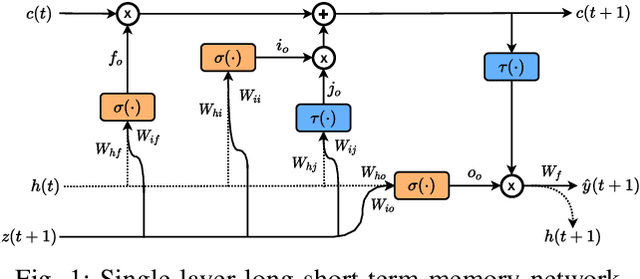
This paper proposes a sparse Bayesian treatment of deep neural networks (DNNs) for system identification. Although DNNs show impressive approximation ability in various fields, several challenges still exist for system identification problems. First, DNNs are known to be too complex that they can easily overfit the training data. Second, the selection of the input regressors for system identification is nontrivial. Third, uncertainty quantification of the model parameters and predictions are necessary. The proposed Bayesian approach offers a principled way to alleviate the above challenges by marginal likelihood/model evidence approximation and structured group sparsity-inducing priors construction. The identification algorithm is derived as an iterative regularized optimization procedure that can be solved as efficiently as training typical DNNs. Furthermore, a practical calculation approach based on the Monte-Carlo integration method is derived to quantify the uncertainty of the parameters and predictions. The effectiveness of the proposed Bayesian approach is demonstrated on several linear and nonlinear systems identification benchmarks with achieving good and competitive simulation accuracy.

A Sparse Bayesian Deep Learning Approach for Identification of Cascaded Tanks Benchmark

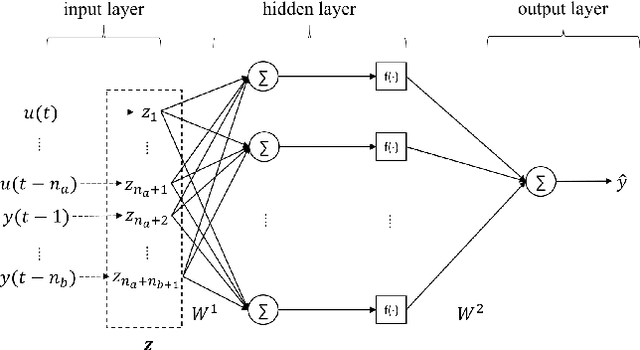
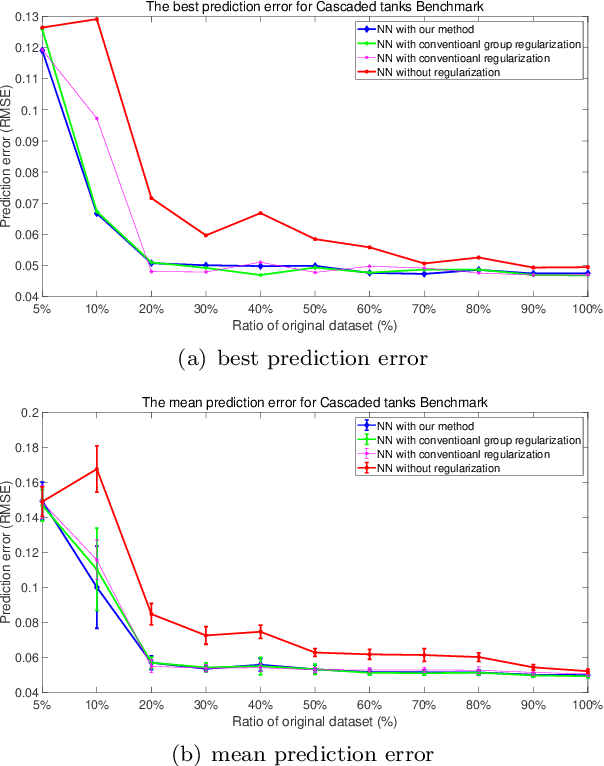
Nonlinear system identification is important with a wide range of applications. The typical approaches for nonlinear system identification include Volterra series models, nonlinear autoregressive with exogenous inputs models, block-structured models, state-space models and neural network models. Among them, neural networks (NN) is an important black-box method thanks to its universal approximation capability and less dependency on prior information. However, there are several challenges associated with NN. The first one lies in the design of a proper neural network structure. A relatively simple network cannot approximate the feature of the system, while a complex model may lead to overfitting. The second lies in the availability of data for some nonlinear systems. For some systems, it is difficult to collect enough data to train a neural network. This raises the challenge that how to train a neural network for system identification with a small dataset. In addition, if the uncertainty of the NN parameter could be obtained, it would be also beneficial for further analysis. In this paper, we propose a sparse Bayesian deep learning approach to address the above problems. Specifically, the Bayesian method can reinforce the regularization on neural networks by introducing introduced sparsity-inducing priors. The Bayesian method can also compute the uncertainty of the NN parameter. An efficient iterative re-weighted algorithm is presented in this paper. We also test the capacity of our method to identify the system on various ratios of the original dataset. The one-step-ahead prediction experiment on Cascaded Tank System shows the effectiveness of our method. Furthermore, we test our algorithm with more challenging simulation experiment on this benchmark, which also outperforms other methods.

BayesNAS: A Bayesian Approach for Neural Architecture Search

One-Shot Neural Architecture Search (NAS) is a promising method to significantly reduce search time without any separate training. It can be treated as a Network Compression problem on the architecture parameters from an over-parameterized network. However, there are two issues associated with most one-shot NAS methods. First, dependencies between a node and its predecessors and successors are often disregarded which result in improper treatment over zero operations. Second, architecture parameters pruning based on their magnitude is questionable. In this paper, we employ the classic Bayesian learning approach to alleviate these two issues by modeling architecture parameters using hierarchical automatic relevance determination (HARD) priors. Unlike other NAS methods, we train the over-parameterized network for only one epoch then update the architecture. Impressively, this enabled us to find the architecture in both proxy and proxyless tasks on CIFAR-10 within only 0.2 GPU days using a single GPU. As a byproduct, our approach can be transferred directly to compress convolutional neural networks by enforcing structural sparsity which achieves extremely sparse networks without accuracy deterioration.