Sparse Bayesian Deep Learning for Dynamic System Identification

This paper proposes a sparse Bayesian treatment of deep neural networks (DNNs) for system identification. Although DNNs show impressive approximation ability in various fields, several challenges still exist for system identification problems. First, DNNs are known to be too complex that they can easily overfit the training data. Second, the selection of the input regressors for system identification is nontrivial. Third, uncertainty quantification of the model parameters and predictions are necessary. The proposed Bayesian approach offers a principled way to alleviate the above challenges by marginal likelihood/model evidence approximation and structured group sparsity-inducing priors construction. The identification algorithm is derived as an iterative regularized optimization procedure that can be solved as efficiently as training typical DNNs. Furthermore, a practical calculation approach based on the Monte-Carlo integration method is derived to quantify the uncertainty of the parameters and predictions. The effectiveness of the proposed Bayesian approach is demonstrated on several linear and nonlinear systems identification benchmarks with achieving good and competitive simulation accuracy.

A Sparse Bayesian Deep Learning Approach for Identification of Cascaded Tanks Benchmark

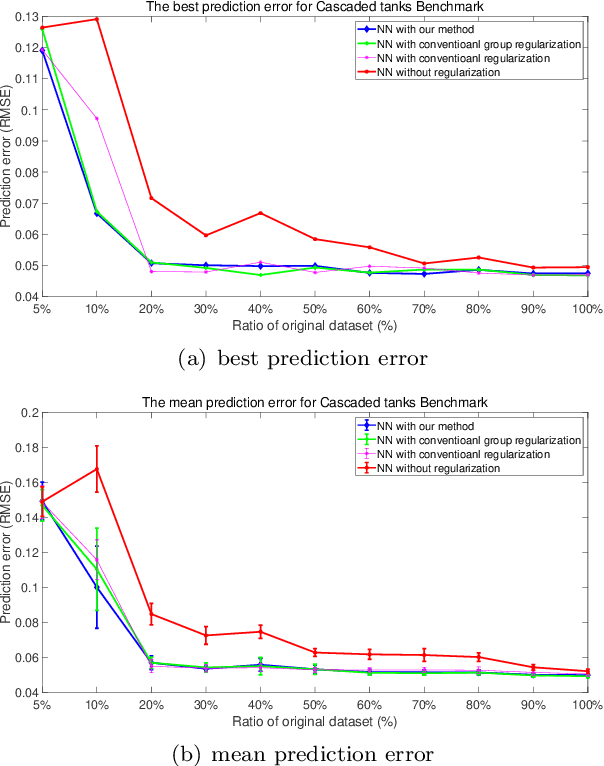
Nonlinear system identification is important with a wide range of applications. The typical approaches for nonlinear system identification include Volterra series models, nonlinear autoregressive with exogenous inputs models, block-structured models, state-space models and neural network models. Among them, neural networks (NN) is an important black-box method thanks to its universal approximation capability and less dependency on prior information. However, there are several challenges associated with NN. The first one lies in the design of a proper neural network structure. A relatively simple network cannot approximate the feature of the system, while a complex model may lead to overfitting. The second lies in the availability of data for some nonlinear systems. For some systems, it is difficult to collect enough data to train a neural network. This raises the challenge that how to train a neural network for system identification with a small dataset. In addition, if the uncertainty of the NN parameter could be obtained, it would be also beneficial for further analysis. In this paper, we propose a sparse Bayesian deep learning approach to address the above problems. Specifically, the Bayesian method can reinforce the regularization on neural networks by introducing introduced sparsity-inducing priors. The Bayesian method can also compute the uncertainty of the NN parameter. An efficient iterative re-weighted algorithm is presented in this paper. We also test the capacity of our method to identify the system on various ratios of the original dataset. The one-step-ahead prediction experiment on Cascaded Tank System shows the effectiveness of our method. Furthermore, we test our algorithm with more challenging simulation experiment on this benchmark, which also outperforms other methods.