Aggressive Quadrotor Flight Using Curiosity-Driven Reinforcement Learning

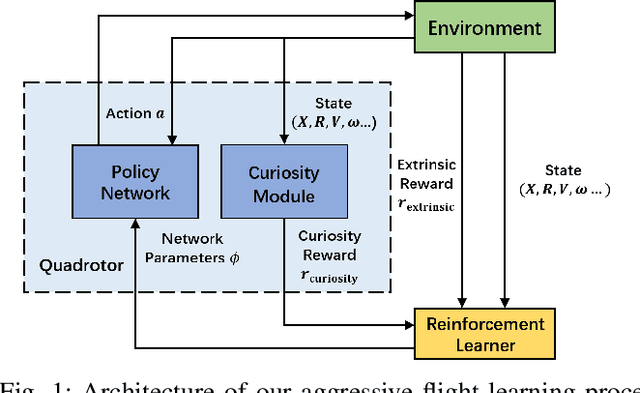
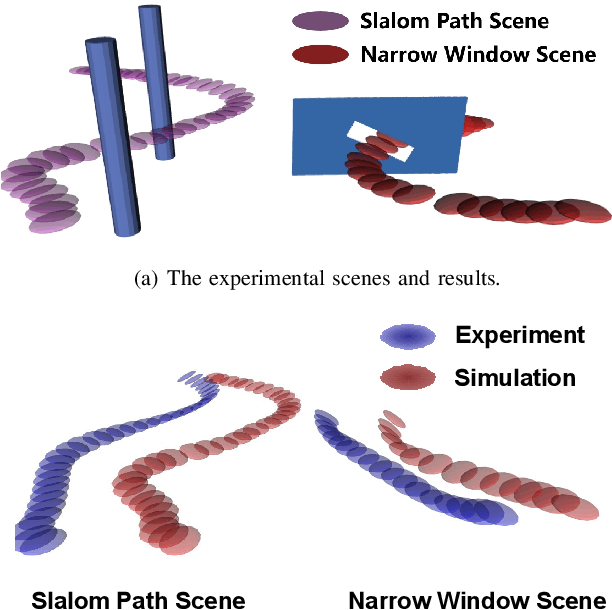
The ability to perform aggressive movements, which are called aggressive flights, is important for quadrotors during navigation. However, aggressive quadrotor flights are still a great challenge to practical applications. The existing solutions to aggressive flights heavily rely on a predefined trajectory, which is a time-consuming preprocessing step. To avoid such path planning, we propose a curiosity-driven reinforcement learning method for aggressive flight missions and a similarity-based curiosity module is introduced to speed up the training procedure. A branch structure exploration (BSE) strategy is also applied to guarantee the robustness of the policy and to ensure the policy trained in simulations can be performed in real-world experiments directly. The experimental results in simulations demonstrate that our reinforcement learning algorithm performs well in aggressive flight tasks, speeds up the convergence process and improves the robustness of the policy. Besides, our algorithm shows a satisfactory simulated to real transferability and performs well in real-world experiments.

Sparse Bayesian Deep Learning for Dynamic System Identification

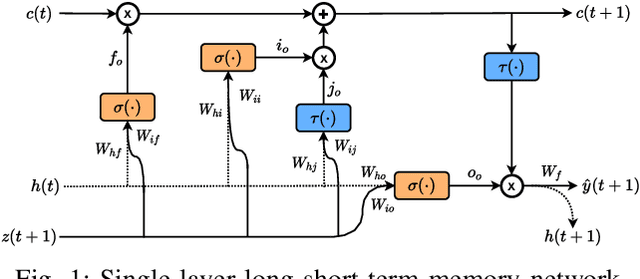
This paper proposes a sparse Bayesian treatment of deep neural networks (DNNs) for system identification. Although DNNs show impressive approximation ability in various fields, several challenges still exist for system identification problems. First, DNNs are known to be too complex that they can easily overfit the training data. Second, the selection of the input regressors for system identification is nontrivial. Third, uncertainty quantification of the model parameters and predictions are necessary. The proposed Bayesian approach offers a principled way to alleviate the above challenges by marginal likelihood/model evidence approximation and structured group sparsity-inducing priors construction. The identification algorithm is derived as an iterative regularized optimization procedure that can be solved as efficiently as training typical DNNs. Furthermore, a practical calculation approach based on the Monte-Carlo integration method is derived to quantify the uncertainty of the parameters and predictions. The effectiveness of the proposed Bayesian approach is demonstrated on several linear and nonlinear systems identification benchmarks with achieving good and competitive simulation accuracy.