Blockwise Principal Component Analysis for monotone missing data imputation and dimensionality reduction

Monotone missing data is a common problem in data analysis. However, imputation combined with dimensionality reduction can be computationally expensive, especially with the increasing size of datasets. To address this issue, we propose a Blockwise principal component analysis Imputation (BPI) framework for dimensionality reduction and imputation of monotone missing data. The framework conducts Principal Component Analysis (PCA) on the observed part of each monotone block of the data and then imputes on merging the obtained principal components using a chosen imputation technique. BPI can work with various imputation techniques and can significantly reduce imputation time compared to conducting dimensionality reduction after imputation. This makes it a practical and efficient approach for large datasets with monotone missing data. Our experiments validate the improvement in speed. In addition, our experiments also show that while applying MICE imputation directly on missing data may not yield convergence, applying BPI with MICE for the data may lead to convergence.

Principle Components Analysis based frameworks for efficient missing data imputation algorithms

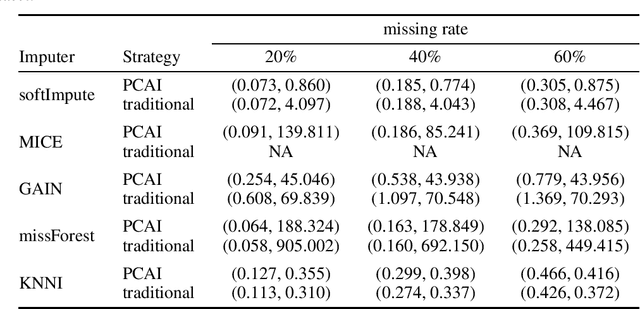
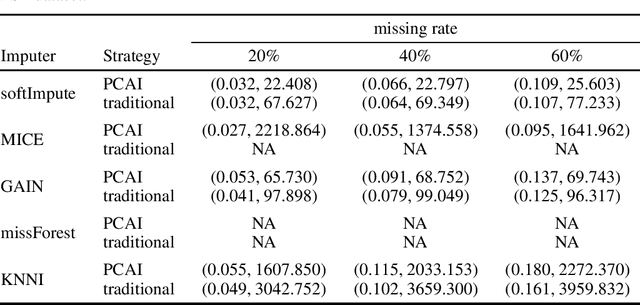
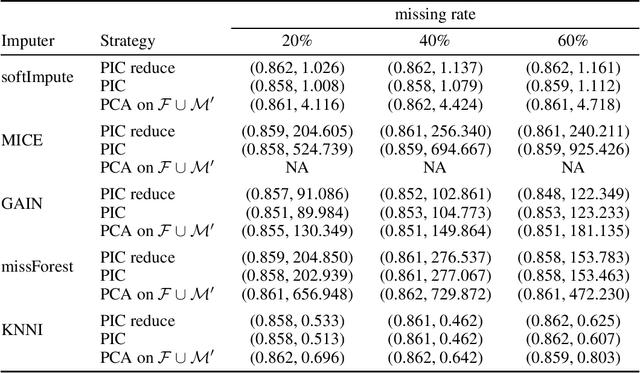
Missing data is a commonly occurring problem in practice, and imputation, i.e., filling the missing entries of the data, is a popular way to deal with this problem. This motivates multiple works on imputation to deal with missing data of various types and dimensions. However, for high-dimensional datasets, these imputation methods can be computationally expensive. Therefore, in this work, we propose Principle Component Analysis Imputation (PCAI), a simple framework based on Principle Component Analysis (PCA) to speed up the imputation process of many available imputation techniques. Next, based on PCAI, we propose PCA Imputation - Classification (PIC), an imputation-dimension reduction-classification framework to deal with missing data classification problems where it is desirable to reduce the dimensions before training a classification model. Our experiments show that the proposed frameworks can be utilized with various imputation algorithms and improve the imputation speed significantly. Interestingly, the frameworks aid imputation methods that rely on many parameters by reducing the dimension of the data and hence, reducing the number of parameters needed to be estimated. Moreover, they not only can achieve compatible mean square error/higher classification accuracy compared to the traditional imputation style on the original missing dataset but many times deliver even better results. In addition, the frameworks also help to tackle the memory issue that many imputation approaches have by reducing the number of features.