Helmut G. Katzgraber
Applying a Random-Key Optimizer on Mixed Integer Programs
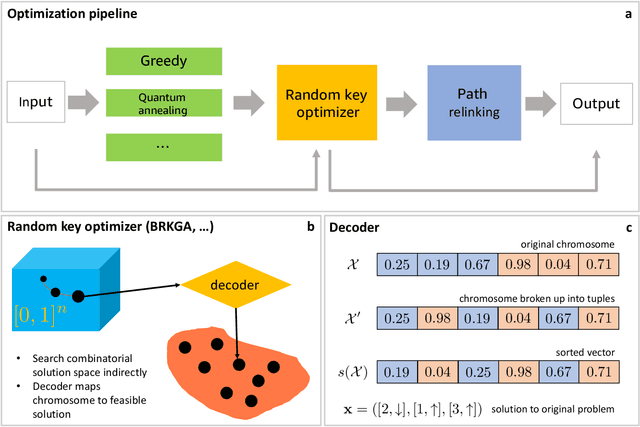
Feb 25, 2026Abstract:Mixed-Integer Programs (MIPs) are NP-hard optimization models that arise in a broad range of decision-making applications, including finance, logistics, energy systems, and network design. Although modern commercial solvers have achieved remarkable progress and perform effectively on many small- and medium-sized instances, their performance often degrades when confronted with large-cale or highly constrained formulations. This paper explores the use of the Random-Key Optimizer (RKO) framework as a flexible, metaheuristic alternative for computing high-quality solutions to MIPs through the design of problem-specific decoders. The proposed approach separates the search process from feasibility enforcement by operating in a continuous random-key space while mapping candidate solutions to feasible integer solutions via efficient decoding procedures. We evaluate the methodology on two representative and structurally distinct benchmark problems: the mean-variance Markowitz portfolio optimization problem with buy-in and cardinality constraints, and the Time-Dependent Traveling Salesman Problem. For each formulation, tailored decoders are developed to reduce the effective search space, promote feasibility, and accelerate convergence. Computational experiments demonstrate that RKO consistently produces competitive, and in several cases superior, solutions compared to a state-of-the-art commercial MIP solver, both in terms of solution quality and computational time. These results highlight the potential of RKO as a scalable and versatile heuristic framework for tackling challenging large-scale MIPs.
Scalable iterative pruning of large language and vision models using block coordinate descent
Nov 26, 2024
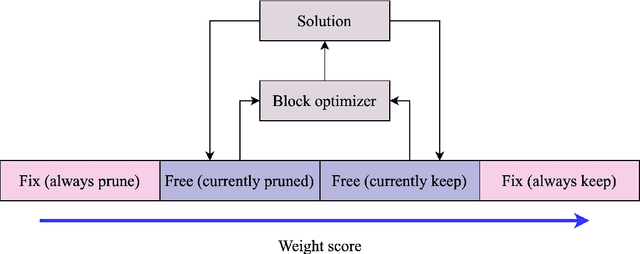
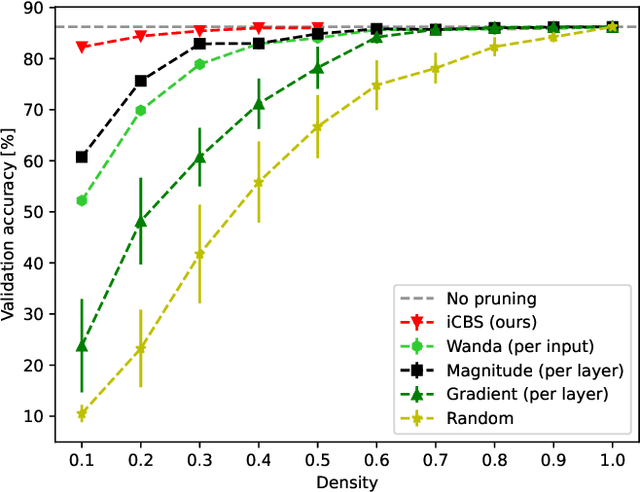
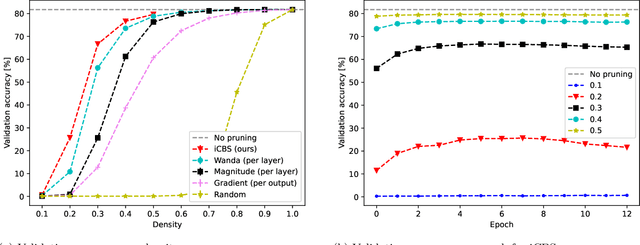
Abstract:Pruning neural networks, which involves removing a fraction of their weights, can often maintain high accuracy while significantly reducing model complexity, at least up to a certain limit. We present a neural network pruning technique that builds upon the Combinatorial Brain Surgeon, but solves an optimization problem over a subset of the network weights in an iterative, block-wise manner using block coordinate descent. The iterative, block-based nature of this pruning technique, which we dub ``iterative Combinatorial Brain Surgeon'' (iCBS) allows for scalability to very large models, including large language models (LLMs), that may not be feasible with a one-shot combinatorial optimization approach. When applied to large models like Mistral and DeiT, iCBS achieves higher performance metrics at the same density levels compared to existing pruning methods such as Wanda. This demonstrates the effectiveness of this iterative, block-wise pruning method in compressing and optimizing the performance of large deep learning models, even while optimizing over only a small fraction of the weights. Moreover, our approach allows for a quality-time (or cost) tradeoff that is not available when using a one-shot pruning technique alone. The block-wise formulation of the optimization problem enables the use of hardware accelerators, potentially offsetting the increased computational costs compared to one-shot pruning methods like Wanda. In particular, the optimization problem solved for each block is quantum-amenable in that it could, in principle, be solved by a quantum computer.
Explainable AI using expressive Boolean formulas
Jun 06, 2023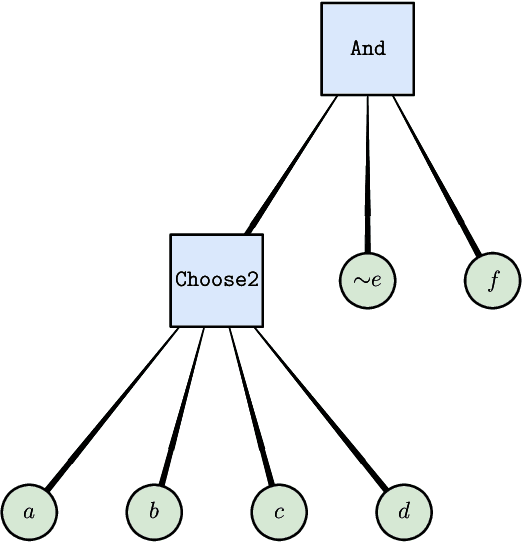
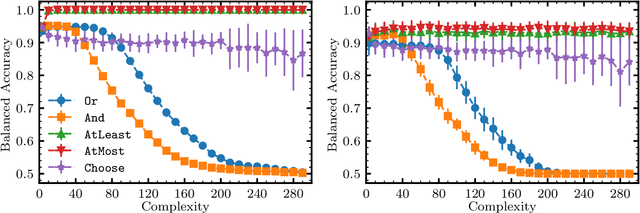
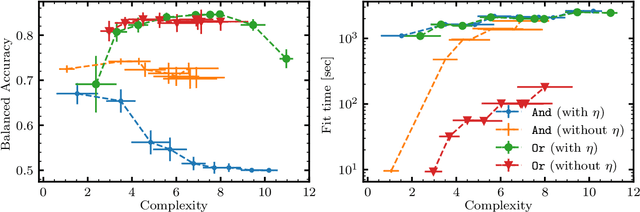
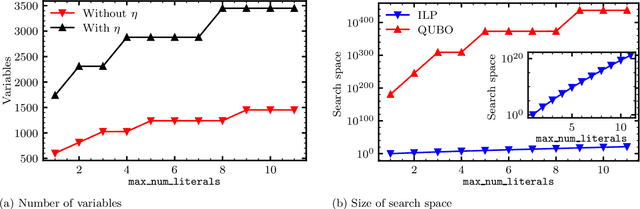
Abstract:We propose and implement an interpretable machine learning classification model for Explainable AI (XAI) based on expressive Boolean formulas. Potential applications include credit scoring and diagnosis of medical conditions. The Boolean formula defines a rule with tunable complexity (or interpretability), according to which input data are classified. Such a formula can include any operator that can be applied to one or more Boolean variables, thus providing higher expressivity compared to more rigid rule-based and tree-based approaches. The classifier is trained using native local optimization techniques, efficiently searching the space of feasible formulas. Shallow rules can be determined by fast Integer Linear Programming (ILP) or Quadratic Unconstrained Binary Optimization (QUBO) solvers, potentially powered by special purpose hardware or quantum devices. We combine the expressivity and efficiency of the native local optimizer with the fast operation of these devices by executing non-local moves that optimize over subtrees of the full Boolean formula. We provide extensive numerical benchmarking results featuring several baselines on well-known public datasets. Based on the results, we find that the native local rule classifier is generally competitive with the other classifiers. The addition of non-local moves achieves similar results with fewer iterations, and therefore using specialized or quantum hardware could lead to a speedup by fast proposal of non-local moves.
Reply to: Modern graph neural networks do worse than classical greedy algorithms in solving combinatorial optimization problems like maximum independent set
Feb 03, 2023Abstract:We provide a comprehensive reply to the comment written by Chiara Angelini and Federico Ricci-Tersenghi [arXiv:2206.13211] and argue that the comment singles out one particular non-representative example problem, entirely focusing on the maximum independent set (MIS) on sparse graphs, for which greedy algorithms are expected to perform well. Conversely, we highlight the broader algorithmic development underlying our original work, and (within our original framework) provide additional numerical results showing sizable improvements over our original results, thereby refuting the comment's performance statements. We also provide results showing run-time scaling superior to the results provided by Angelini and Ricci-Tersenghi. Furthermore, we show that the proposed set of random d-regular graphs does not provide a universal set of benchmark instances, nor do greedy heuristics provide a universal algorithmic baseline. Finally, we argue that the internal (parallel) anatomy of graph neural networks is very different from the (sequential) nature of greedy algorithms and emphasize that graph neural networks have demonstrated their potential for superior scalability compared to existing heuristics such as parallel tempering. We conclude by discussing the conceptual novelty of our work and outline some potential extensions.
* Manuscript: 3 pages, 2 figures
Optimization of Robot Trajectory Planning with Nature-Inspired and Hybrid Quantum Algorithms
Jun 08, 2022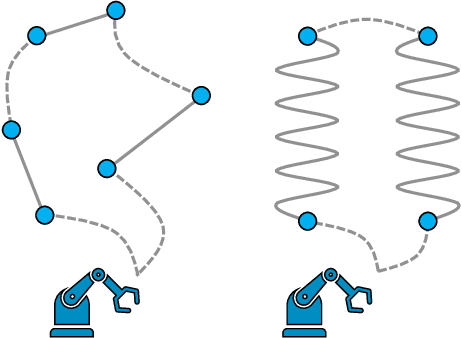
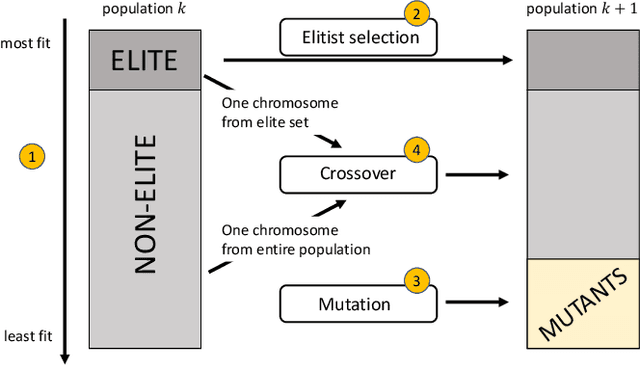
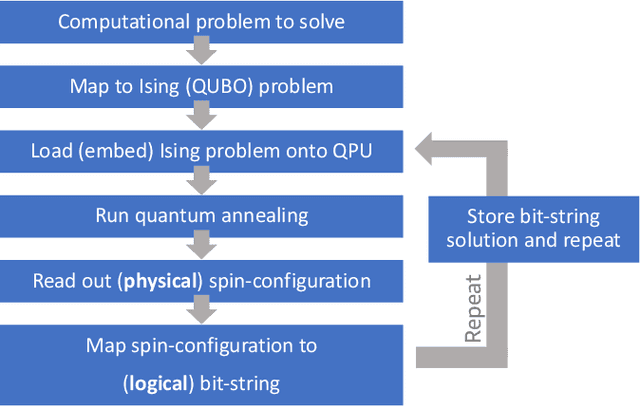
Abstract:We solve robot trajectory planning problems at industry-relevant scales. Our end-to-end solution integrates highly versatile random-key algorithms with model stacking and ensemble techniques, as well as path relinking for solution refinement. The core optimization module consists of a biased random-key genetic algorithm. Through a distinct separation of problem-independent and problem-dependent modules, we achieve an efficient problem representation, with a native encoding of constraints. We show that generalizations to alternative algorithmic paradigms such as simulated annealing are straightforward. We provide numerical benchmark results for industry-scale data sets. Our approach is found to consistently outperform greedy baseline results. To assess the capabilities of today's quantum hardware, we complement the classical approach with results obtained on quantum annealing hardware, using qbsolv on Amazon Braket. Finally, we show how the latter can be integrated into our larger pipeline, providing a quantum-ready hybrid solution to the problem.
Graph Coloring with Physics-Inspired Graph Neural Networks
Feb 03, 2022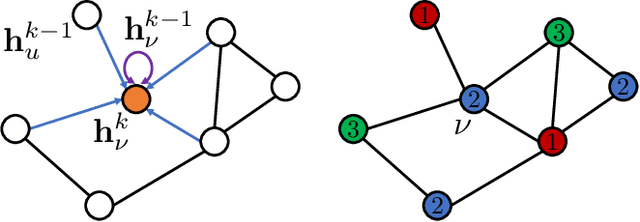
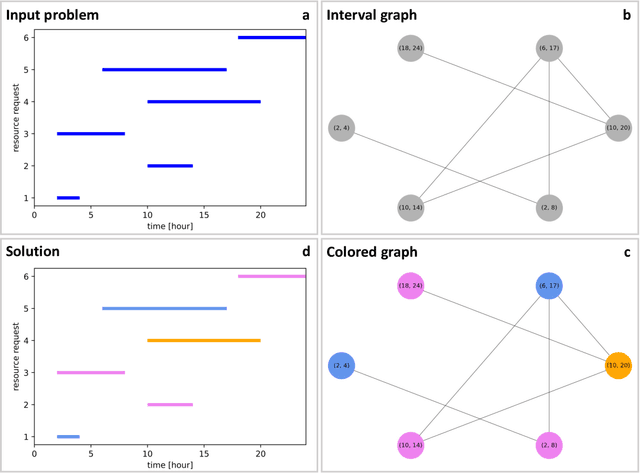
Abstract:We show how graph neural networks can be used to solve the canonical graph coloring problem. We frame graph coloring as a multi-class node classification problem and utilize an unsupervised training strategy based on the statistical physics Potts model. Generalizations to other multi-class problems such as community detection, data clustering, and the minimum clique cover problem are straightforward. We provide numerical benchmark results and illustrate our approach with an end-to-end application for a real-world scheduling use case within a comprehensive encode-process-decode framework. Our optimization approach performs on par or outperforms existing solvers, with the ability to scale to problems with millions of variables.
Combinatorial Optimization with Physics-Inspired Graph Neural Networks
Jul 02, 2021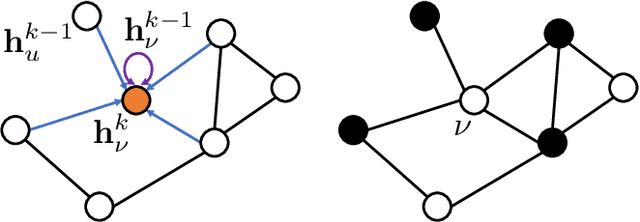
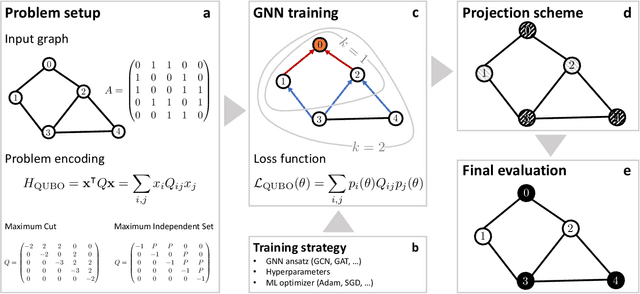
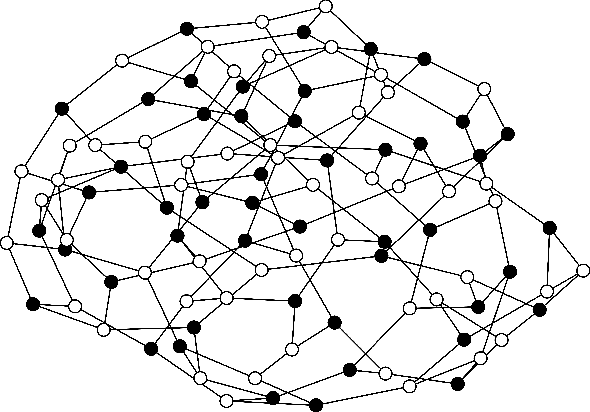
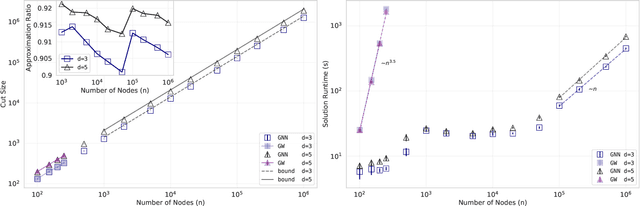
Abstract:We demonstrate how graph neural networks can be used to solve combinatorial optimization problems. Our approach is broadly applicable to canonical NP-hard problems in the form of quadratic unconstrained binary optimization problems, such as maximum cut, minimum vertex cover, maximum independent set, as well as Ising spin glasses and higher-order generalizations thereof in the form of polynomial unconstrained binary optimization problems. We apply a relaxation strategy to the problem Hamiltonian to generate a differentiable loss function with which we train the graph neural network and apply a simple projection to integer variables once the unsupervised training process has completed. We showcase our approach with numerical results for the canonical maximum cut and maximum independent set problems. We find that the graph neural network optimizer performs on par or outperforms existing solvers, with the ability to scale beyond the state of the art to problems with millions of variables.
Evolutionary Approaches to Optimization Problems in Chimera Topologies
Aug 17, 2016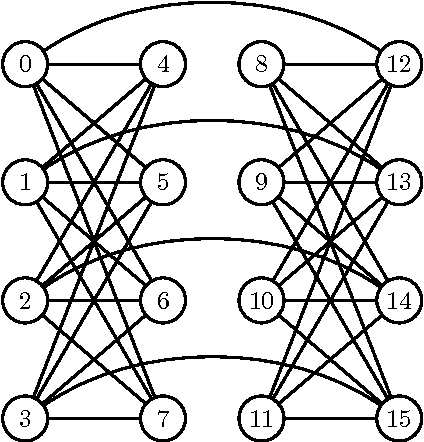
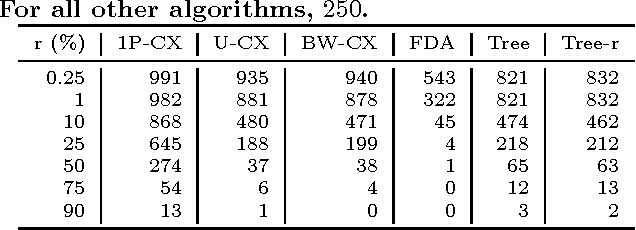
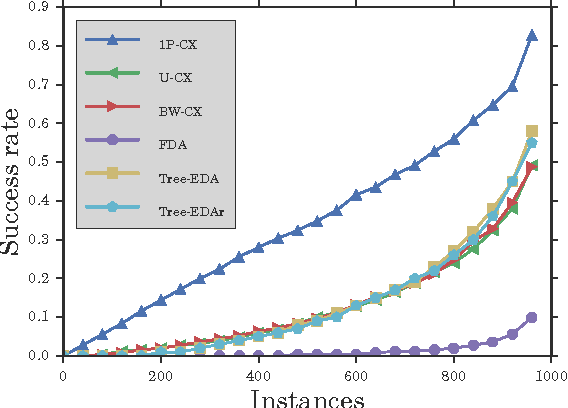
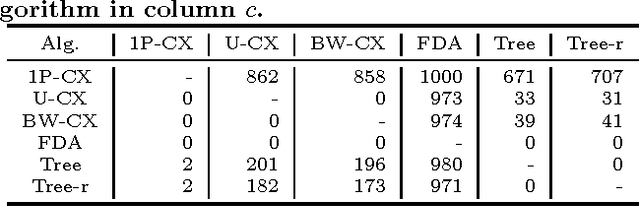
Abstract:Chimera graphs define the topology of one of the first commercially available quantum computers. A variety of optimization problems have been mapped to this topology to evaluate the behavior of quantum enhanced optimization heuristics in relation to other optimizers, being able to efficiently solve problems classically to use them as benchmarks for quantum machines. In this paper we investigate for the first time the use of Evolutionary Algorithms (EAs) on Ising spin glass instances defined on the Chimera topology. Three genetic algorithms (GAs) and three estimation of distribution algorithms (EDAs) are evaluated over $1000$ hard instances of the Ising spin glass constructed from Sidon sets. We focus on determining whether the information about the topology of the graph can be used to improve the results of EAs and on identifying the characteristics of the Ising instances that influence the success rate of GAs and EDAs.
* 8 pages, 5 figures, 3 tables
A probabilistic evolutionary optimization approach to compute quasiparticle braids
Oct 02, 2014


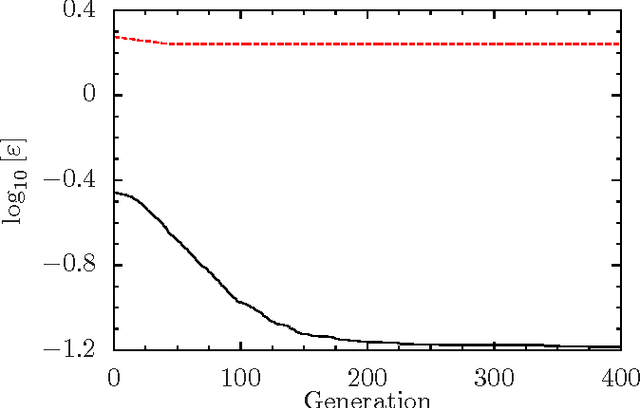
Abstract:Topological quantum computing is an alternative framework for avoiding the quantum decoherence problem in quantum computation. The problem of executing a gate in this framework can be posed as the problem of braiding quasiparticles. Because these are not Abelian, the problem can be reduced to finding an optimal product of braid generators where the optimality is defined in terms of the gate approximation and the braid's length. In this paper we propose the use of different variants of estimation of distribution algorithms to deal with the problem. Furthermore, we investigate how the regularities of the braid optimization problem can be translated into statistical regularities by means of the Boltzmann distribution. We show that our best algorithm is able to produce many solutions that approximates the target gate with an accuracy in the order of $10^{-6}$, and have lengths up to 9 times shorter than those expected from braids of the same accuracy obtained with other methods.
* 9 pages,7 figures. Accepted at SEAL 2014
Genetic braid optimization: A heuristic approach to compute quasiparticle braids
Feb 13, 2013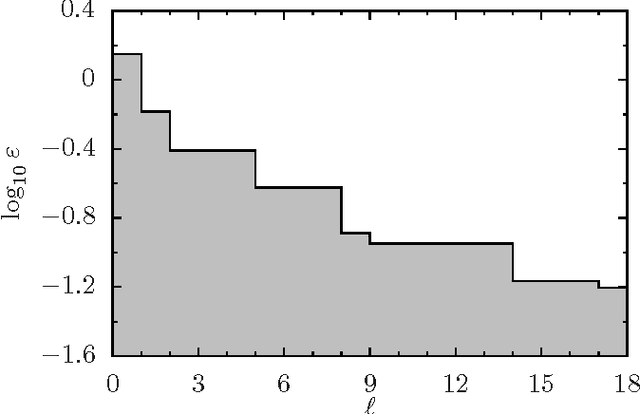

Abstract:In topologically-protected quantum computation, quantum gates can be carried out by adiabatically braiding two-dimensional quasiparticles, reminiscent of entangled world lines. Bonesteel et al. [Phys. Rev. Lett. 95, 140503 (2005)], as well as Leijnse and Flensberg [Phys. Rev. B 86, 104511 (2012)] recently provided schemes for computing quantum gates from quasiparticle braids. Mathematically, the problem of executing a gate becomes that of finding a product of the generators (matrices) in that set that approximates the gate best, up to an error. To date, efficient methods to compute these gates only strive to optimize for accuracy. We explore the possibility of using a generic approach applicable to a variety of braiding problems based on evolutionary (genetic) algorithms. The method efficiently finds optimal braids while allowing the user to optimize for the relative utilities of accuracy and/or length. Furthermore, when optimizing for error only, the method can quickly produce efficient braids.
* 6 pages 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge