Evolutionary Approaches to Optimization Problems in Chimera Topologies
Paper and Code
Aug 17, 2016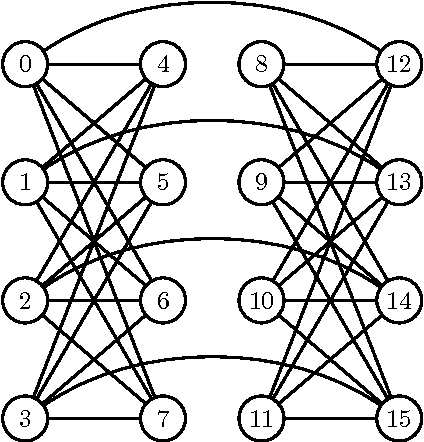
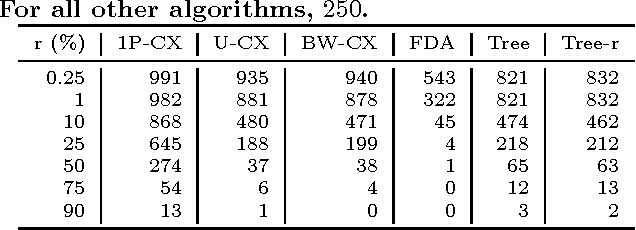
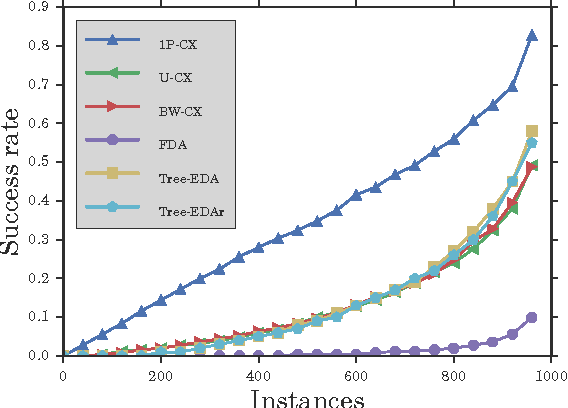
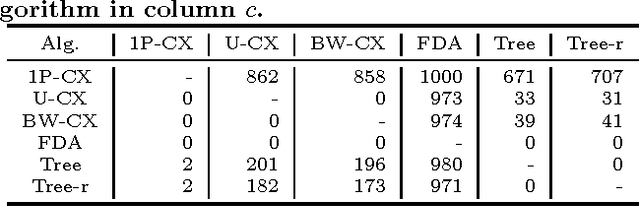
Chimera graphs define the topology of one of the first commercially available quantum computers. A variety of optimization problems have been mapped to this topology to evaluate the behavior of quantum enhanced optimization heuristics in relation to other optimizers, being able to efficiently solve problems classically to use them as benchmarks for quantum machines. In this paper we investigate for the first time the use of Evolutionary Algorithms (EAs) on Ising spin glass instances defined on the Chimera topology. Three genetic algorithms (GAs) and three estimation of distribution algorithms (EDAs) are evaluated over $1000$ hard instances of the Ising spin glass constructed from Sidon sets. We focus on determining whether the information about the topology of the graph can be used to improve the results of EAs and on identifying the characteristics of the Ising instances that influence the success rate of GAs and EDAs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge