Scalable iterative pruning of large language and vision models using block coordinate descent

Pruning neural networks, which involves removing a fraction of their weights, can often maintain high accuracy while significantly reducing model complexity, at least up to a certain limit. We present a neural network pruning technique that builds upon the Combinatorial Brain Surgeon, but solves an optimization problem over a subset of the network weights in an iterative, block-wise manner using block coordinate descent. The iterative, block-based nature of this pruning technique, which we dub ``iterative Combinatorial Brain Surgeon'' (iCBS) allows for scalability to very large models, including large language models (LLMs), that may not be feasible with a one-shot combinatorial optimization approach. When applied to large models like Mistral and DeiT, iCBS achieves higher performance metrics at the same density levels compared to existing pruning methods such as Wanda. This demonstrates the effectiveness of this iterative, block-wise pruning method in compressing and optimizing the performance of large deep learning models, even while optimizing over only a small fraction of the weights. Moreover, our approach allows for a quality-time (or cost) tradeoff that is not available when using a one-shot pruning technique alone. The block-wise formulation of the optimization problem enables the use of hardware accelerators, potentially offsetting the increased computational costs compared to one-shot pruning methods like Wanda. In particular, the optimization problem solved for each block is quantum-amenable in that it could, in principle, be solved by a quantum computer.

Explainable AI using expressive Boolean formulas

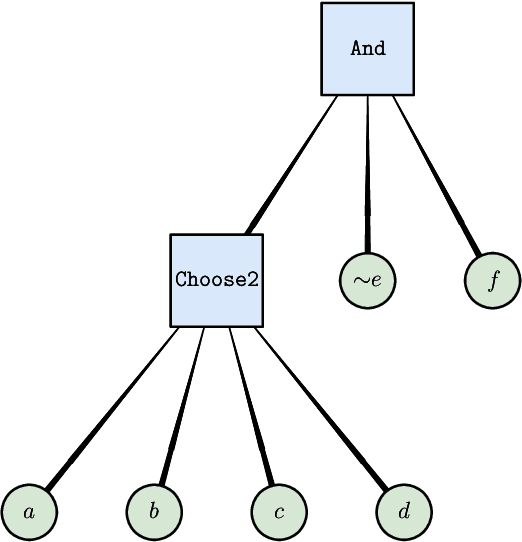
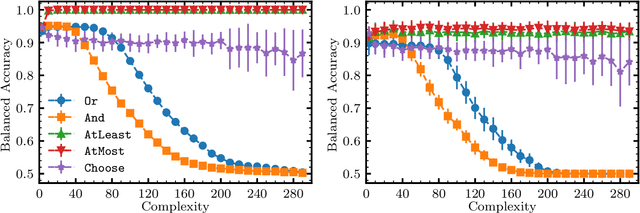
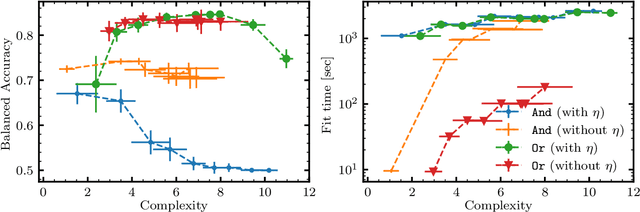
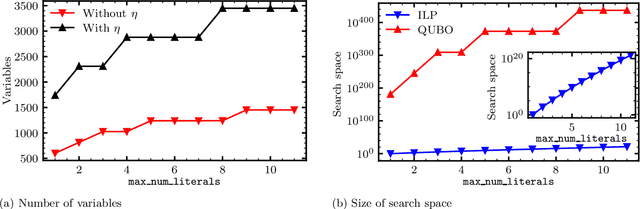
We propose and implement an interpretable machine learning classification model for Explainable AI (XAI) based on expressive Boolean formulas. Potential applications include credit scoring and diagnosis of medical conditions. The Boolean formula defines a rule with tunable complexity (or interpretability), according to which input data are classified. Such a formula can include any operator that can be applied to one or more Boolean variables, thus providing higher expressivity compared to more rigid rule-based and tree-based approaches. The classifier is trained using native local optimization techniques, efficiently searching the space of feasible formulas. Shallow rules can be determined by fast Integer Linear Programming (ILP) or Quadratic Unconstrained Binary Optimization (QUBO) solvers, potentially powered by special purpose hardware or quantum devices. We combine the expressivity and efficiency of the native local optimizer with the fast operation of these devices by executing non-local moves that optimize over subtrees of the full Boolean formula. We provide extensive numerical benchmarking results featuring several baselines on well-known public datasets. Based on the results, we find that the native local rule classifier is generally competitive with the other classifiers. The addition of non-local moves achieves similar results with fewer iterations, and therefore using specialized or quantum hardware could lead to a speedup by fast proposal of non-local moves.