Explainable AI using expressive Boolean formulas

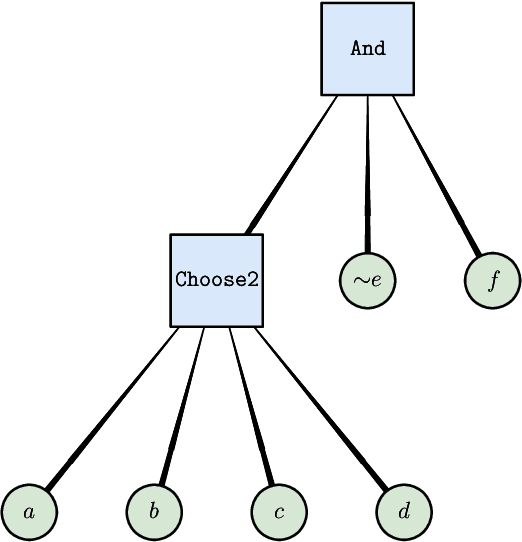
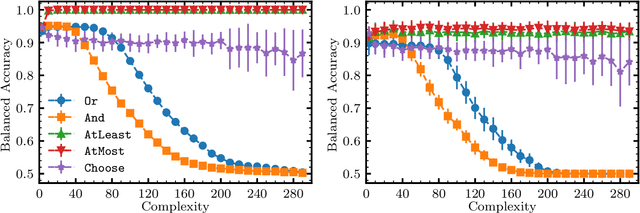
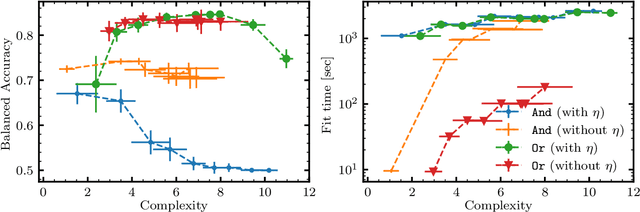
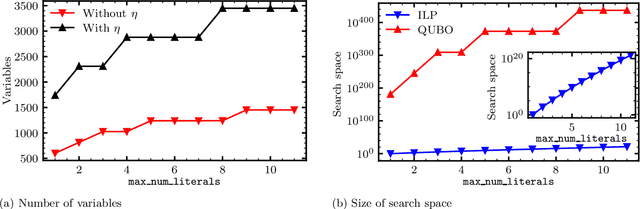
We propose and implement an interpretable machine learning classification model for Explainable AI (XAI) based on expressive Boolean formulas. Potential applications include credit scoring and diagnosis of medical conditions. The Boolean formula defines a rule with tunable complexity (or interpretability), according to which input data are classified. Such a formula can include any operator that can be applied to one or more Boolean variables, thus providing higher expressivity compared to more rigid rule-based and tree-based approaches. The classifier is trained using native local optimization techniques, efficiently searching the space of feasible formulas. Shallow rules can be determined by fast Integer Linear Programming (ILP) or Quadratic Unconstrained Binary Optimization (QUBO) solvers, potentially powered by special purpose hardware or quantum devices. We combine the expressivity and efficiency of the native local optimizer with the fast operation of these devices by executing non-local moves that optimize over subtrees of the full Boolean formula. We provide extensive numerical benchmarking results featuring several baselines on well-known public datasets. Based on the results, we find that the native local rule classifier is generally competitive with the other classifiers. The addition of non-local moves achieves similar results with fewer iterations, and therefore using specialized or quantum hardware could lead to a speedup by fast proposal of non-local moves.

Graph Coloring with Physics-Inspired Graph Neural Networks

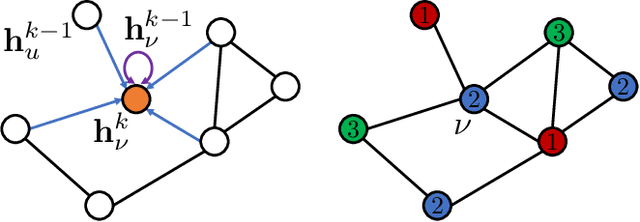
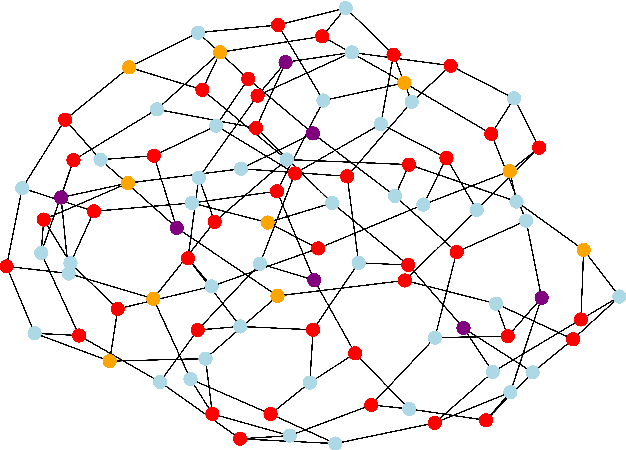
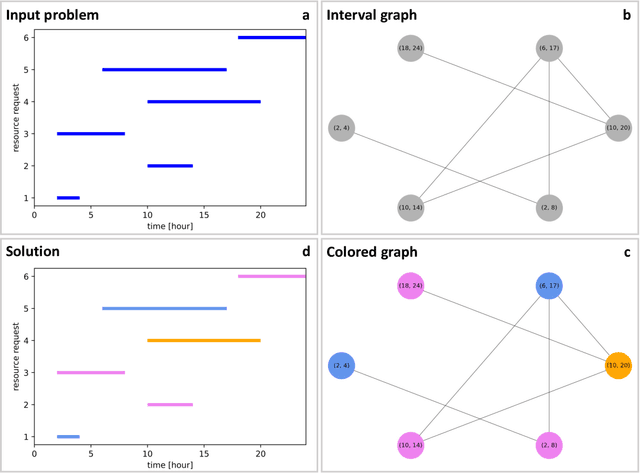
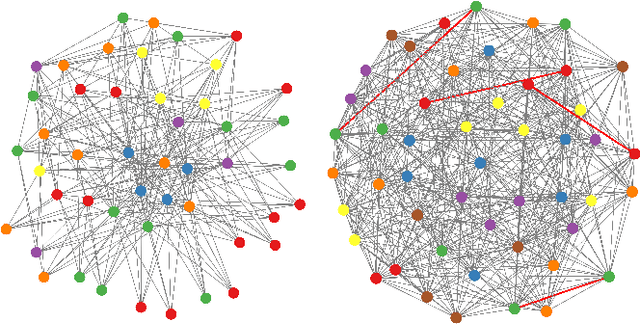
We show how graph neural networks can be used to solve the canonical graph coloring problem. We frame graph coloring as a multi-class node classification problem and utilize an unsupervised training strategy based on the statistical physics Potts model. Generalizations to other multi-class problems such as community detection, data clustering, and the minimum clique cover problem are straightforward. We provide numerical benchmark results and illustrate our approach with an end-to-end application for a real-world scheduling use case within a comprehensive encode-process-decode framework. Our optimization approach performs on par or outperforms existing solvers, with the ability to scale to problems with millions of variables.